Question

If the point $P(a^2,a)$
lies in the region corresponding to the acute angle between the lines $2y=x$
and $4y=x$
, then find the values of $a\stackrel{.}{}$

Answer

`alpha in (2,4)`

Explanation

Acute angle is formed by lines in first the third quadrants.

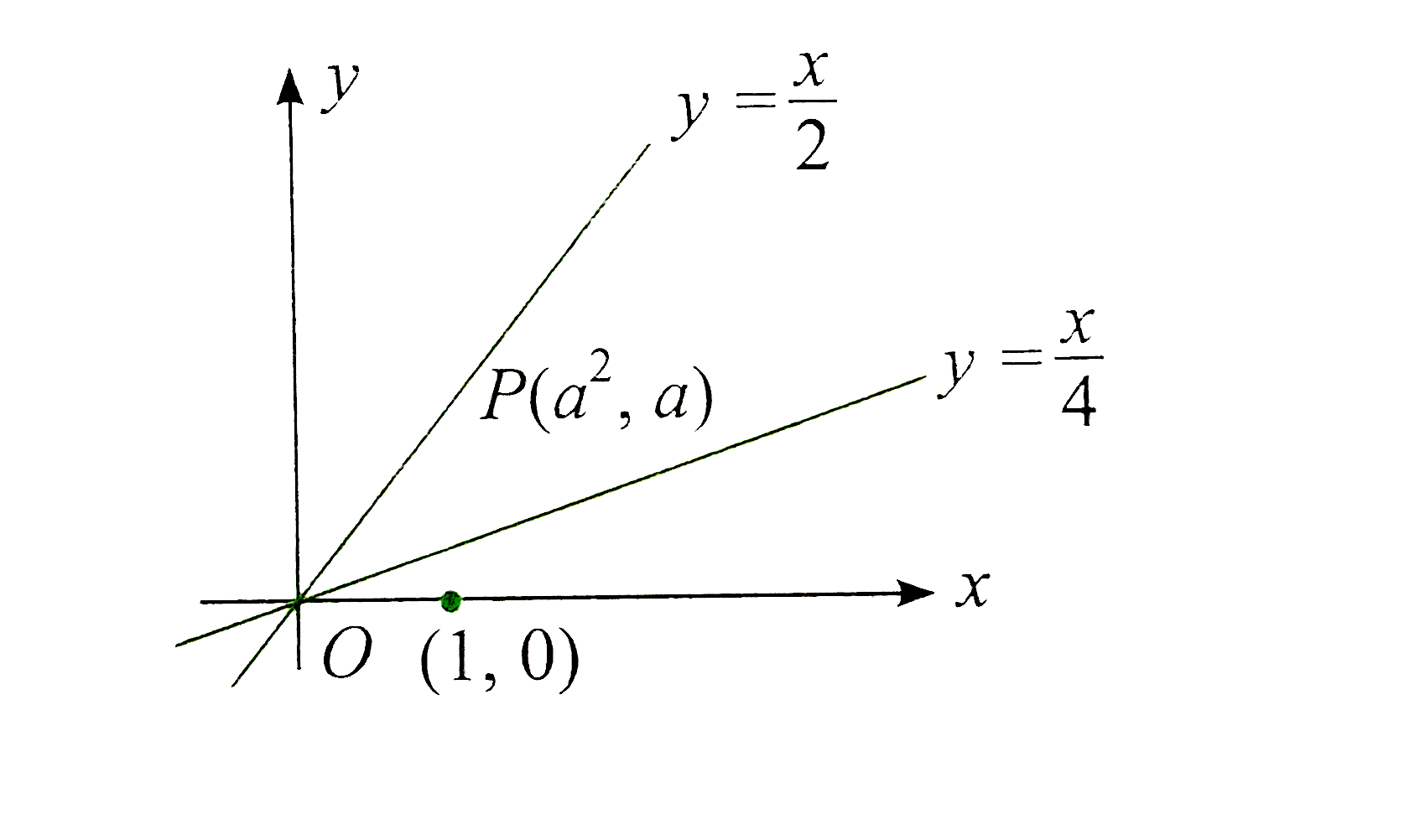
But `a^(2) gt 0, " and hence, point " P(a^(2),a)` lies in the first quadrant.
`"We have "a-(a^(2))/(4) gt 0 " and " a-(a^(2))/(2) lt 0`
`rArr a in (0,4) " and " a in (-oo, 0) uu (2, oo )`
`rArr a in (2,4)`