Question

If (a, 3a) is a variable point lying above the straight line 2x+y+4 =0 and below the line x+4y-8=0, then find the values of a.

Answer

`-4//5 lt a lt 8//13`

Explanation

We have lines
`2x+y+4=0 " " (1)`
`" and " x+4y-8=0 " " (2)`
Lines are drawn as shown in the following figure.

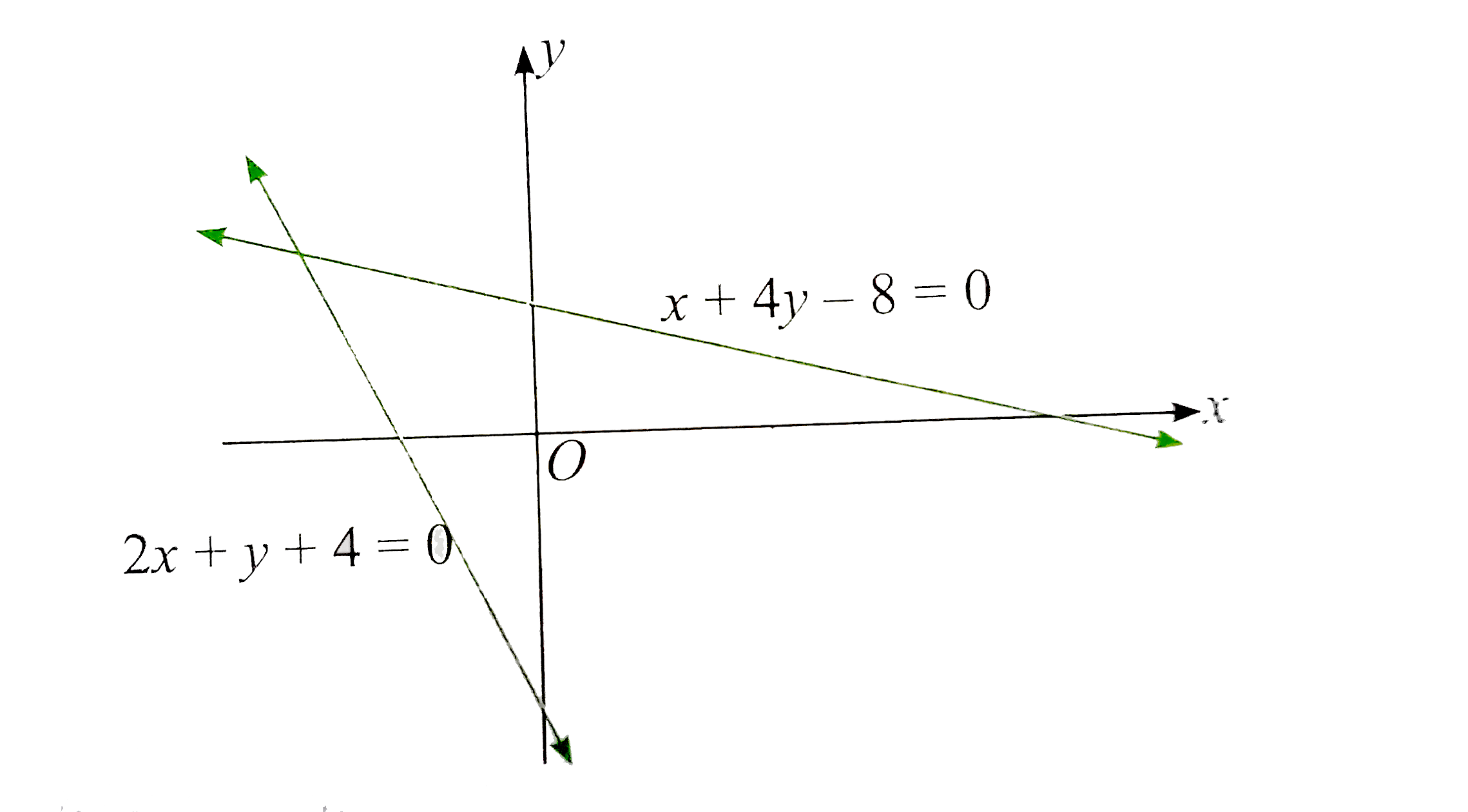
`"Let "L_(1)(x,y) = 2x+y+4`
`"and "L_(2)(x,y) = x+4y-8`
`" "L_(1)(0,0) = 4 gt 0`
So, (a,3a) lies above the first line if
`" "L_(1)(a,3a) = 2a+3a+ 4 gt 0`
`"or "a gt -4//5 " " (3)`
`" " L_(2)(0,0) = -8 lt 0`
So, (a,3a) lies below the second line if
`L_(2)(a,3a) = a+12a-8 lt 0`
`" or " a lt 8//13 " " (4)`
From (3) and (4),
`-4//5 lt a lt 8//13`