A square of side 'a' lies above the x-axis and has one vertex at the origin. The side passing through the origin makes an angle $α$ (0 < $α' <$ pi/4 ) with the positive direction of x-axis. Find the equation of diagonal not passing through the origin ?

A

$y (cos α + sin α) + x (sin α - cos α) = a$

B

$y (cos α + sin α) + x (sin α + cos α) = a$

C

$y (cos α + sin α) + x (cos α - sin α) = a$

D

$y (cos α - sin α) - x (sin α - cos α) = a$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

The coordinates of A and B are as shown in the figure.

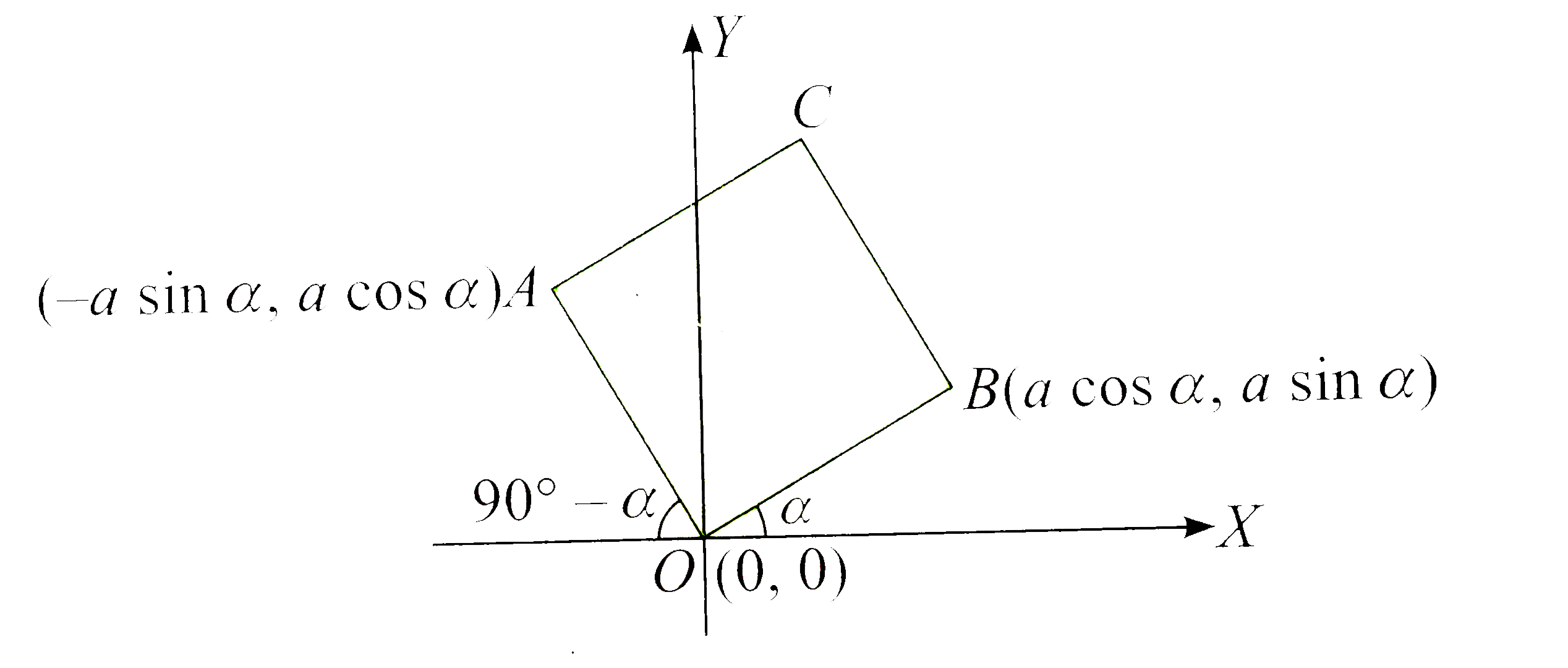
The equation of the diagonal AB is
$y - a sin α = \frac{a cos α - a sin α}{- a sin α - a cos α} (x - a cos α)$
$or y (cos α + sin α) - a (sin α cos α + {sin}^{2} α)$
$= - (cos α - sin α) x + a cos α (cos α - sin α)$
$y (cos α + sin α) + x (cos α - sin α) = a$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A square of side 'a' lies above the x-axis and has one vertex at the origin. The side passing through the origin makes an angle $α$ (0 < $α' <$ pi/4 ) with the positive direction of x-axis. Find the equation of diagonal not passing through the origin ?
A $y (cos α - sin α) - x (sin α - cos α) = α$
B $y (cos α + sin α) - x (sin α - cos α) = a$
C $y (cos α - sin α) + x (sin α + cos α) = α$
D $y (cos α + sin α) + x (cos α - sin α) = α$
Question 2 - Select One
A square of side a lies above the X- axis and has one vertex at the origin . The side passing through the origin makes an angle $π / 6$ with the positive direction of X-axis .The equation of its diagonal not passing through the origin is
A $y (\sqrt{3} - 1) - x (1 - \sqrt{3}) = 2 a$
B $y (\sqrt{3} + 1) + x (1 - \sqrt{3}) = 2 a$
C $y (\sqrt{3} + 1) + x (1 + \sqrt{3}) = 2 a$
D $y (\sqrt{3} + 1) + x (\sqrt{3} - 1) = 2 a$
Question 3 - Select One
A square of each side 2, lies above the x-axis and has one vertex at the origin. If one of the sides passing through the origin makes an angle $30^{\circ}$ with the positive direction of the x-axis, then the sum of the x-coordinates of the vertices of the square is:
A $\sqrt{3} - 2$
B $2 \sqrt{3} - 1$
C $\sqrt{3} - 1$
D $2 \sqrt{3} - 2$

CENGAGE-STRAIGHT LINES-Exercise (Single)

Home
Ask Doubt
Profile