Question

Consider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The distance between the orthocenter and the circumcenter of triangle PQR is

Options

A. `25//2`
B. `29//2`
C. `37//2`
D. `51//2`

Answer

A

Explanation

Since the triangle is right-angled, the circumcenter is the midpoint of PQ and the orthocenter is R(1, -7). Hence,

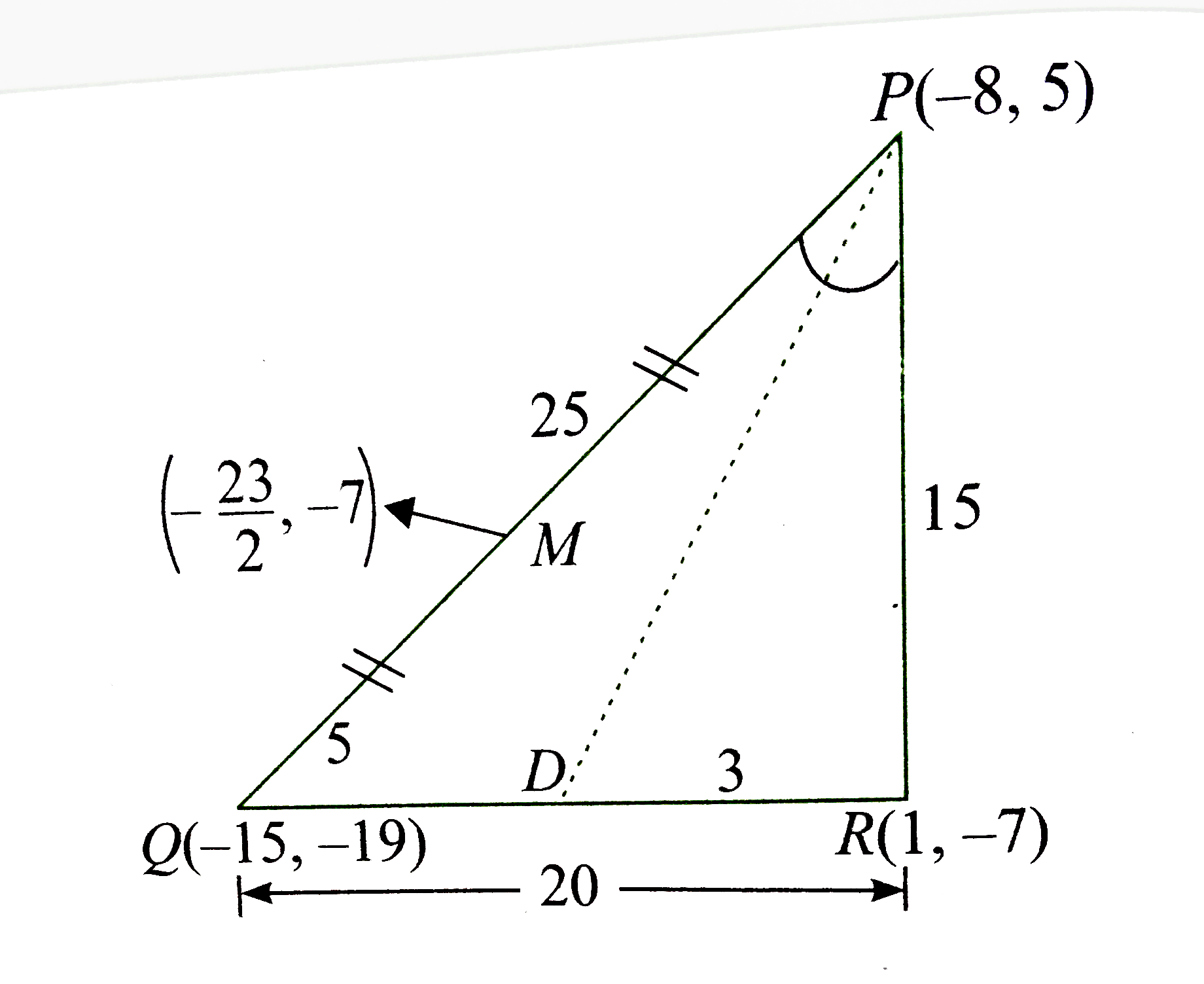
`RM = |sqrt(((23)/(2) + 1)^(2))| = 12(1)/(2)`