The base of an isosceles triangle measures 4 units base angle is equal to . A straight line cuts the extension of the base at a point M at the angle and bisects the lateral side of the triangle which is nearest to M.
The possible range of values in which area of quadrilateral which straight line cuts off from the given triangle lie in
(4,3)
(4,5)
(3,4)
The correct Answer is:D
For the given specification of the triangle, consider triangle ABC as shown in the figure.
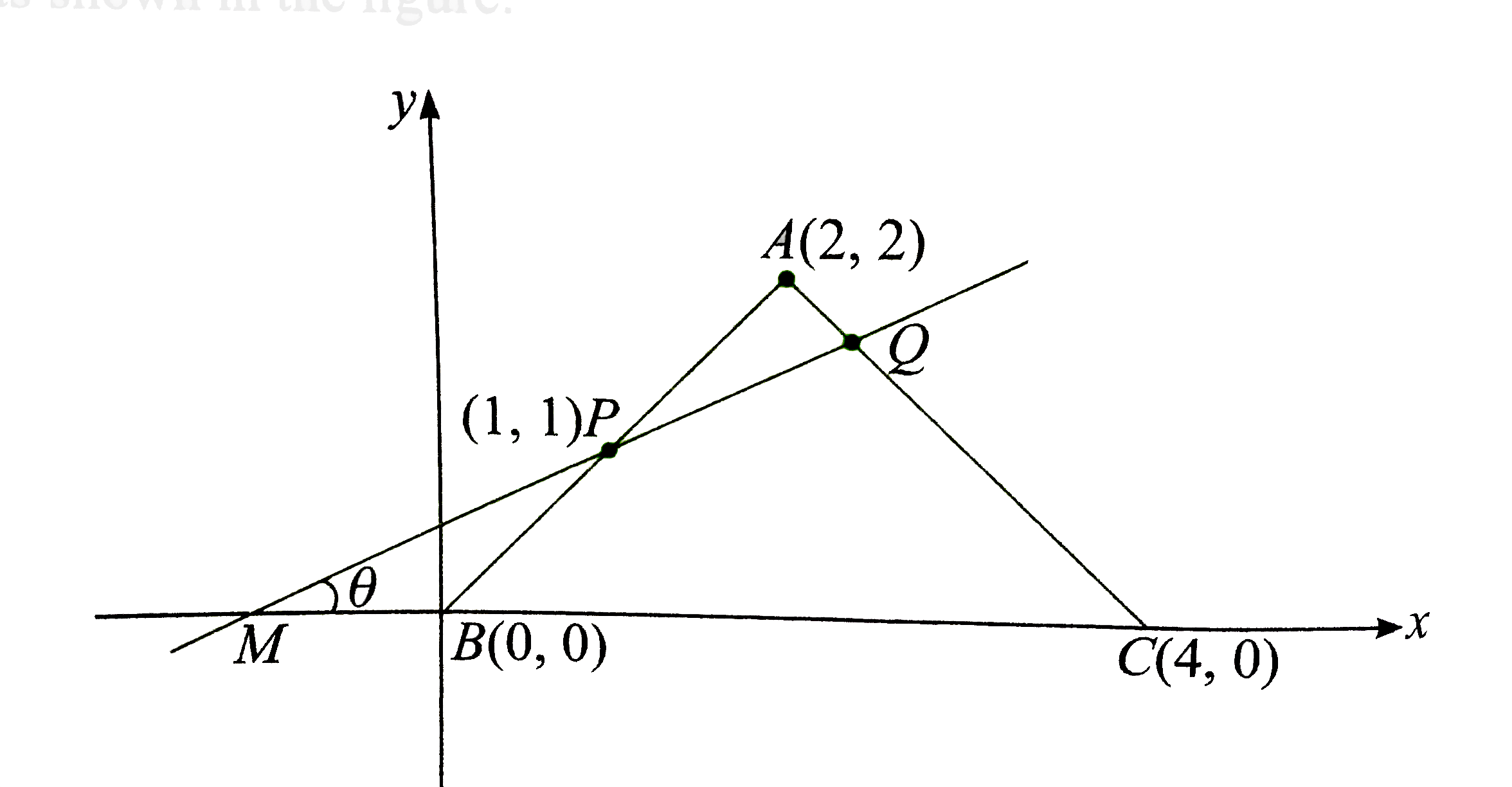
Equation of line PM is
For point Q, solving MP and AC,
Area of quadilateral BPQC,
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Matrix)
8 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Numerical)
13 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
The base of an isosceles triangle measures 4 units base angle is equal to 45∘. A straight line cuts the extension of the base at a point M at the angle θ and bisects the lateral side of the triangle which is nearest to M.
The area of quadrilateral which the straight line cuts off from the given triangle is
View SolutionThe base of an isosceles triangle measures 4 units base angle is equal to 45∘. A straight line cuts the extension of the base at a point M at the angle θ and bisects the lateral side of the triangle which is nearest to M.
The length of portion of straight line inside the triangle may lie in the range
View Solution
Knowledge Check
The base of an isosceles triangle measures 4 units base angle is equal to 45∘. A straight line cuts the extension of the base at a point M at the angle θ and bisects the lateral side of the triangle which is nearest to M.
The area of quadrilateral which the straight line cuts off from the given triangle isA3+tanθ1+tanθB3+5tanθ1+tanθC3+tanθ1−tanθD3+2tanθ1+tanθThe base of an isosceles triangle measures 4 units base angle is equal to 45∘. A straight line cuts the extension of the base at a point M at the angle θ and bisects the lateral side of the triangle which is nearest to M.
The length of portion of straight line inside the triangle may lie in the rangeA(2,4)B(32,√3)C(√2,2)D(√2,√3)In an isosceles triangle with base angle α and lateral side 4, Rr=
A8cosαB8cosα1−cosαC8cosα1+cosαD8cosα−(1−cosα)
Prove that the straight line joining the vertex of an isosceles triangle to any point in the base is smaller than either of the equal sides of the triangle.
View SolutionThe perimeter of an isosceles triangle is 42cm and its base is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
View SolutionThe perimeter of an isosceles triangle is 42cm and its base is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
View SolutionThe lateral sides of an isosceles triangle with vertex angle 90∘ are 12cm each. Find the area of the triangle and hence its base
View SolutionIf the straight line which bisects the vertical angle of a triangle is perpendicular to the base, the triangle is:
View Solution
