Given four collinear points P, Q, R and S list all the line segments determined by them
Step by step video & image solution for Given four collinear points P, Q, R and S list all the line segments determined by them by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
What do you mean by collinear points ?
How many lines can you draw passing through three collinear points ?
Given three collinear points A,B and C . How many line segments do they determine ? Name them.
View SolutionGiven two points P and Q , find how many line segments do they deter-mine. Name the line segments determined by the three collinear points P, Q and R.
View SolutionMark the following points on a sheet of paper. Tell how many line segments can be obtained in each case: Two points A, B. Three non-collinear points A, B, C. Four points such that no three of them belong to the same line. Any five points so that on three of them are collinear.
View SolutionMark the following points on a sheet of paper. Tell how many line segments can be obtained in each case: Two points A, B. Three non-collinear points A, B, C. Four points such that no three of them belong to the same line. Any five points so that on three of them are collinear.
View SolutionAre the points P,Q,R shown in the figure given below collinear ?

View SolutionIn the given figure, name:
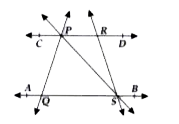
four pairs of intersecting lines four collinear points (iii) three non-collinear points (iv) three lines whose point of intersection is p
View SolutionTake four distinct collinear points A,B,C and D in plane (page of your copy.)
Name the lines segments.
View SolutionThe ends of a line segment are P(1,3)andQ(1,1), R is a point on the line segment PQ such that PR:QR=1:λ.If R is an interior point of the parabola y2=4x then
View SolutionThere are n points in a plane, no 3 of which are collinear and p points are collinear. The number of straight lines by joining them:
View SolutionIn Figure , name the following Figure Five line segments (ii) Five rays Four collinear points Two pairs of non-intersecting line segments.
View Solution
