A particle is projected up an inclines plane. Plane is inclined at an angle $θ$ with horizontal and particle is projected at an angle $α$ with horizontal. If particle strikes the plane horizontally prove that $tan α = 2 tan θ$

Video Solution

Text Solution

Verified by Experts

We know time of flight
$T = \frac{2 u sin (α + θ)}{g cos θ}$
Considering vertical motion
$u = v sin α$
$a = - g$
$v = θ$
$∴ T = \frac{u sin α}{g} = \frac{2 u sin (α - θ)}{g cos θ}$
$sin α cos θ = 2 sin α cos θ - 2 cos α sin θ$
$2 cos α sin θ = sin α cos θ$
$2 tan θ = tan α$

|

Updated on:21/07/2023

Class 12 PHYSICS KINEMATICS-2D

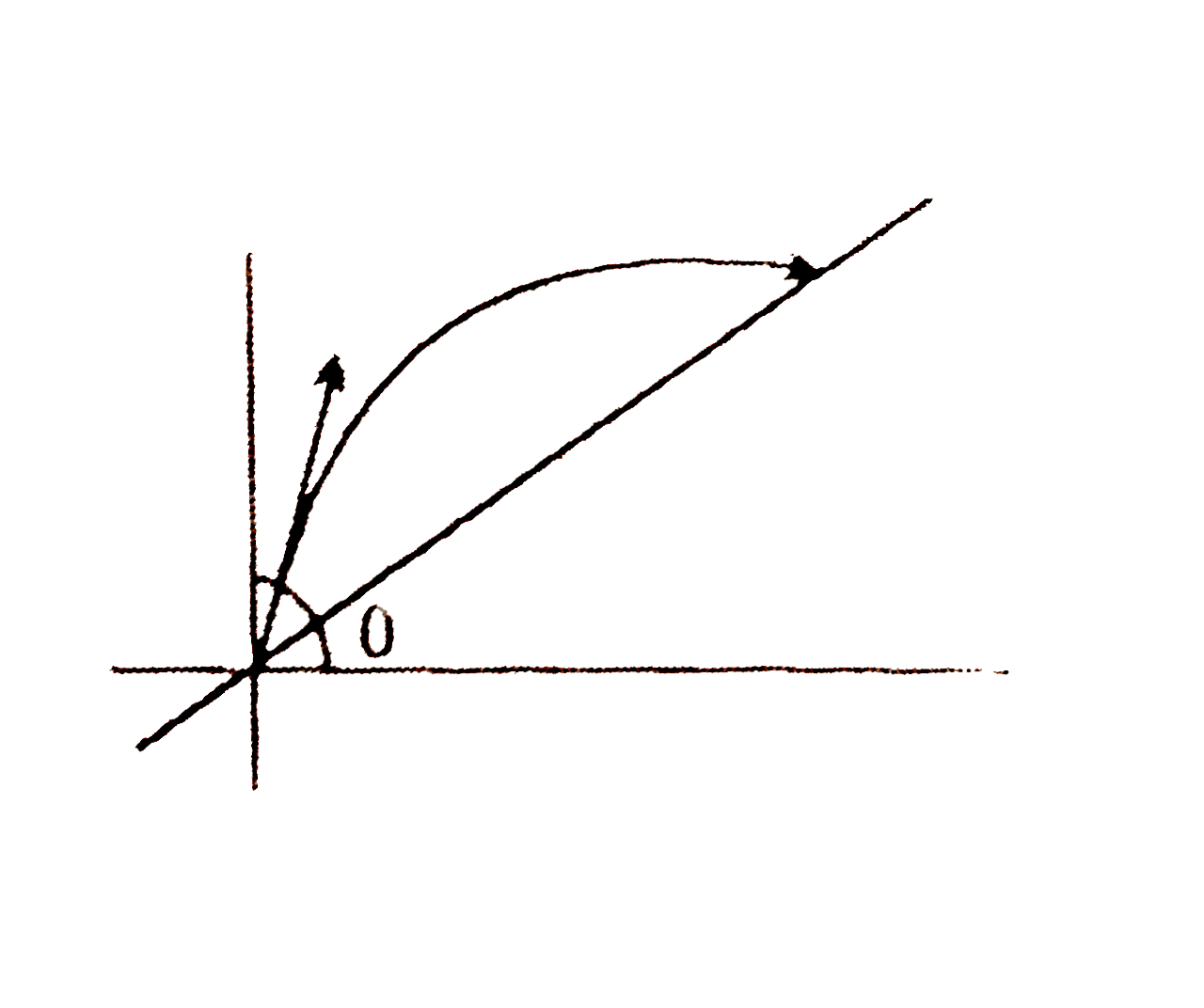
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle I projected at an angle of elevation $α$ after time $t$ it makes an angle $β$ with horizontal. The velocity of projection is
A $\frac{2 g t cos β}{sin (α - β)}$
B $\frac{g t cos β}{sin (α - β)}$
C $\frac{g t}{2 sin (α - β)}$
D $\frac{4 g t}{sin (α - β)}$
Question 2 - Select One
A particle is projected with a certain velocity at an angle $\propto$ above the horizontal from the foot of an inclined plane of inclination $30^{\circ}$ . If the particle strikes the plane normally, then $\propto$ is equal to.
A $30^{\circ} + {tan}^{- 1} (\frac{\sqrt{3}}{2})$
B $45^{\circ}$
C $60^{\circ}$
D $30^{\circ} + {tan}^{- 1} (2 \sqrt{3})$
Question 3 - Select One
a particle is projected down on inclined plane with a velocity of 21m/s at an angle of $60^{\circ}$ with the horizontal its range on the inclined plane inclined at an angle of $30^{\circ}$ with the horizontal is
A21dm
B2.1dm
C30dm
D6dm

ALLEN-KINEMATICS-2D-Exercise (O-2)

Home
Ask Doubt
Profile