A particle is projected up an inclined plane with initial speed v=20m/s at an angle θ=30∘ with plane. The component of its velocity perpendicular to plane when it strikes the plane is
10√3m/s
10m/s
5√3m/s
Data is insufficient
The correct Answer is:B
To solve the problem, we need to find the component of the particle's velocity that is perpendicular to the inclined plane when it strikes the plane. Here's a step-by-step solution:
Step 1: Identify the Initial Conditions
- The initial speed of the particle, v=20m/s.
- The angle of projection with respect to the inclined plane, θ=30∘.
Step 2: Resolve the Initial Velocity
We need to resolve the initial velocity into two components: one parallel to the inclined plane and one perpendicular to the inclined plane.
- The component of the initial velocity perpendicular to the inclined plane (uy) can be calculated using:
uy=vsin(θ)
Substituting the values:
uy=20sin(30∘)=20×12=10m/s
Step 3: Analyze the Motion Perpendicular to the Plane
The motion perpendicular to the inclined plane is influenced by gravity. The acceleration due to gravity acting in the direction perpendicular to the inclined plane is gcos(θ).
- Since the particle is projected upwards, it will first rise to a maximum height where its velocity becomes zero, and then it will fall back down to the inclined plane.
Step 4: Determine the Final Velocity Upon Hitting the Plane
When the particle returns to the inclined plane, the velocity component perpendicular to the plane will be equal in magnitude to the initial velocity component but in the opposite direction.
- Therefore, the final velocity component perpendicular to the plane (vy) when it strikes the plane is:
vy=uy=10m/s
Conclusion
The component of the particle's velocity perpendicular to the inclined plane when it strikes the plane is 10m/s.
- The initial speed of the particle, v=20m/s.
- The angle of projection with respect to the inclined plane, θ=30∘.
We need to resolve the initial velocity into two components: one parallel to the inclined plane and one perpendicular to the inclined plane.
uy=vsin(θ)
Substituting the values:
uy=20sin(30∘)=20×12=10m/s
The motion perpendicular to the inclined plane is influenced by gravity. The acceleration due to gravity acting in the direction perpendicular to the inclined plane is gcos(θ).
When the particle returns to the inclined plane, the velocity component perpendicular to the plane will be equal in magnitude to the initial velocity component but in the opposite direction.
vy=uy=10m/s
The component of the particle's velocity perpendicular to the inclined plane when it strikes the plane is 10m/s.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - MCQ_TYPE23videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - COMPREHENSION_TYPE13videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Subjective Questions24videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
In the above problem, what is the component of its velocity perpendicular to the plane when it strikes at A ?
View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View Solution
Knowledge Check
- Question 1 - Select One
A particle is prjected up an inclined with initial speed v=20m/s at an angle θ=30∘ with the plane. The component of its velocity perpendicular to the plane when it strikes the plane is:
A10√3m/sB10m/sC5√3m/sDdata is insufficient - Question 2 - Select One
A small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘ to the bottom edge of the slope. It returns to the edge after 2s. The ball is in constant with the inclined plane throughout the process. What is the inclination angle of the plane?
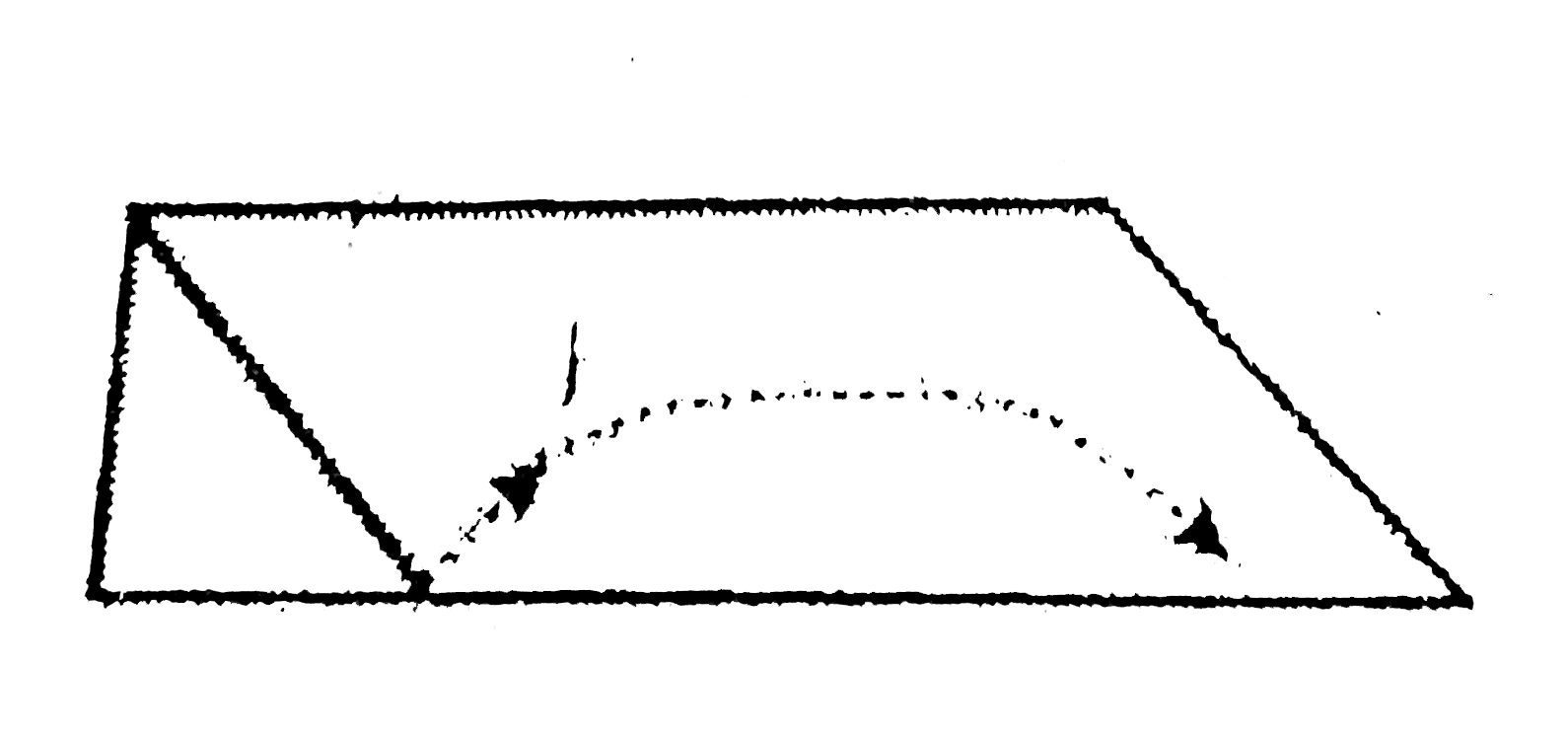 A15∘B60∘C37∘D30∘
A15∘B60∘C37∘D30∘ - Question 3 - Select One
A small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘to the bottom edge of the slope .It returns to the edge after 2s . The ball is in contact with the inclied plane throughout the process. The angle of inclination θ is :−.
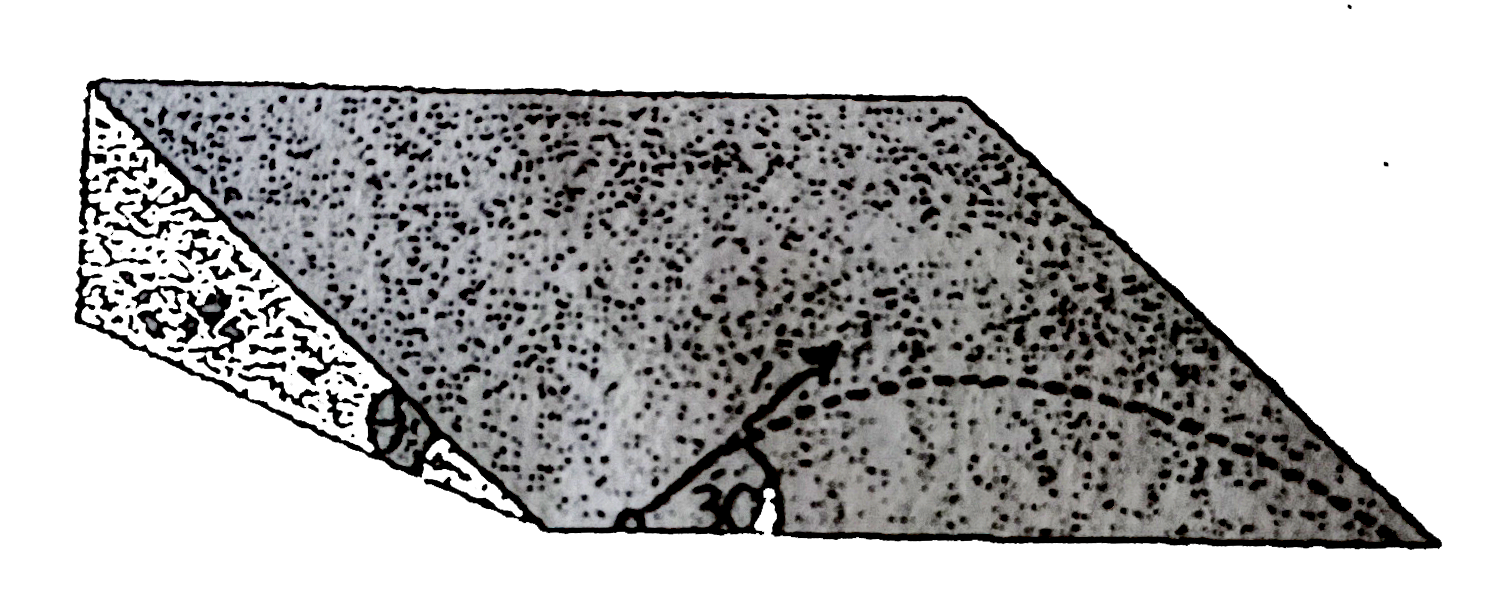 A45∘B53∘C30∘D37∘
A45∘B53∘C30∘D37∘
A plane is inclined at an angle 30∘ with horizontal. The component of a vector →A=−10k perpendicular to this plane is: (here z-direction is vertically upwards)
View SolutionA particle of mass m is projected up from the bottom of an inclined plane with initial velocity v0 at angle 45∘ with an inclined plane of inclineation 30∘ as shown in figure. At the same time a small block of same mass m is released from rest at a height h. The particle hits the block at some point on inclined plane.
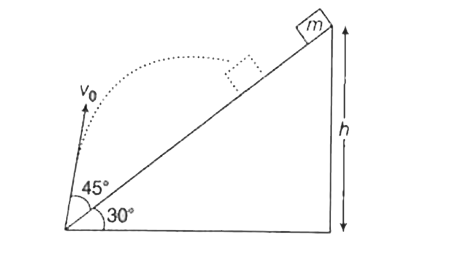
If the particle sticks to the block after collision, the velocity of block parallel to the inclined plane just after collision will be (take g=10m/s2)View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .View Solution
.View Solution
A particle of mass m is projected up from the bottom of an inclined plane with initial velocity v0 at angle 45∘ with an inclined plane of inclination 30∘ as shown in figure. At the same time a small block of same mass m is released from rest at a height h, the particle hits the block at some point on the inclined plane. Neglect friction at inclined.
Q. The value of height h isView Solution
A particle of mass m is projected up from the bottom of an inclined plane with initial velocity v0 at angle 45∘ with an inclined plane of inclination 30∘ as shown in figure. At the same time a small block of same mass m is released from rest at a height h, the particle hits the block at some point on the inclined plane. Neglect friction at inclined.
Q. If the particlee stick to the block after collision the velocity of block parallel tot he inclined plane just after collision will be (take g=10ms2View Solution

