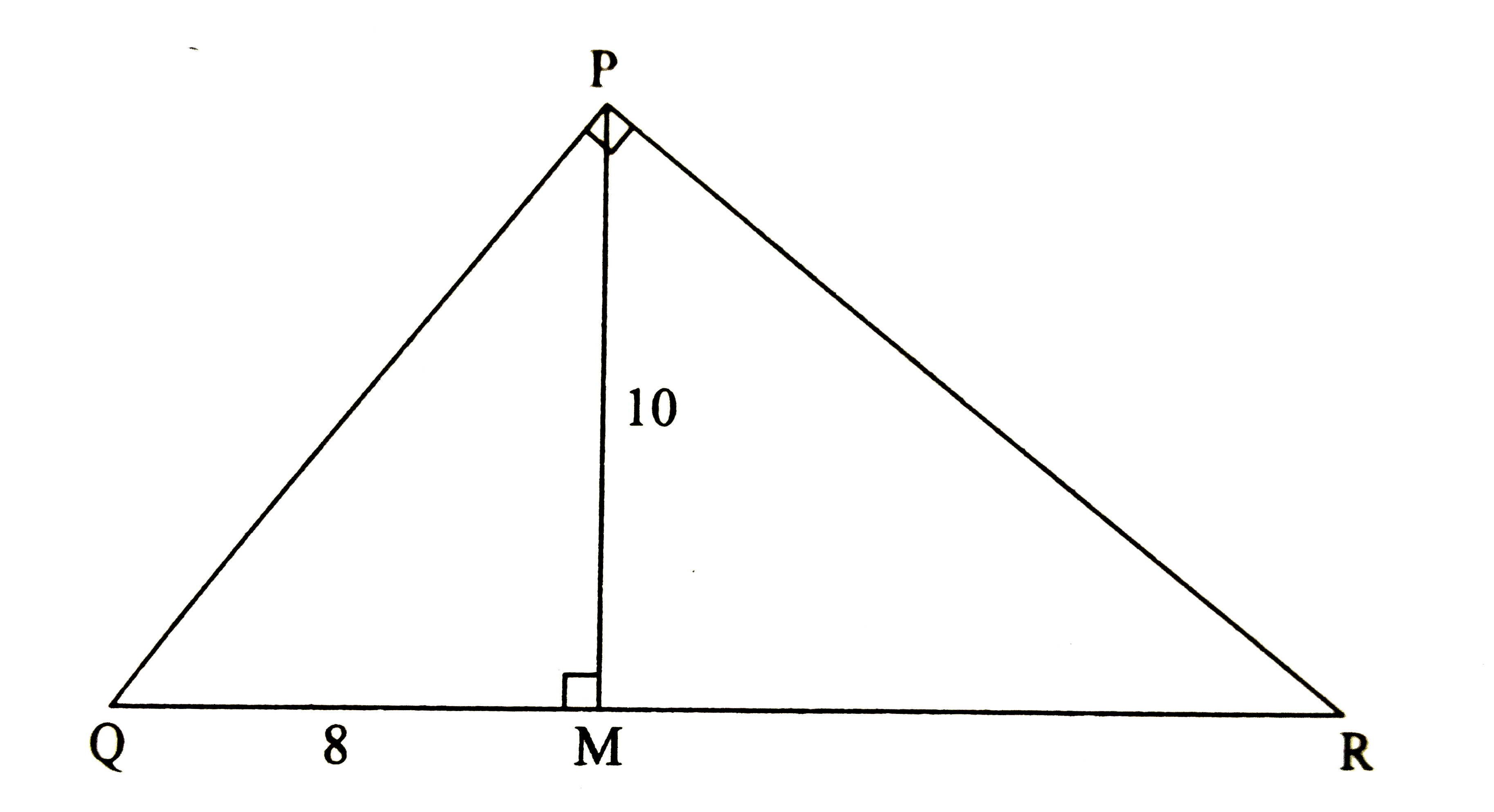
In the adjoining figure, ∠QPR=90∘,segPM⊥ hypotenuse QR, Q - M - R. If PM = 10, QM = 8 then find QR.Solution in Tamil
The correct Answer is:QR = 20.5
Step by step video, text & image solution for In the adjoining figure, angle QPR = 90^(@), "seg" PM bot hypotenuse QR, Q - M - R. If PM = 10, QM = 8 then find QR. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREMBOOK - CHETAN PUBLICATIONCHAPTER - PYTHAGORAS THEOREMEXERCISE - pratice set - 2.1
1 Videos
- PYTHAGORAS THEOREMBOOK - CHETAN PUBLICATIONCHAPTER - PYTHAGORAS THEOREMEXERCISE - Practice Set - 2.2
3 Videos
- MODEL ACTIVITY SHEET BOOK - CHETAN PUBLICATIONCHAPTER - MODEL ACTIVITY SHEET EXERCISE - QUESTION
29 Videos
- QUADRATIC EQUATIONSBOOK - CHETAN PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - ASSIGNMENT
12 Videos
Similar Questions
For finding AB and BC with the help of information in adjoining figure, complete the following activity,AB=BC............ ∴∠BAC=........... ∴AB=BC=........×AC =........× 8 =........×2× 2 =.......
(##CTN_MK_MAT_X_P2_GEO_CO2_SLV_015_Q5.png" width="80%">
View SolutionIn ΔPQRsegPSis median ofΔPQR.AndPT⊥QR,
(i) PR2=PS2+QR×ST+(QR2)2
View SolutionWhat is the ratio of 1mm 1cm ?
View SolutionIf α and β are the roots of quadratic equation 2x2+4x+3=0, then the value of α+β=
View SolutionIn ∠PQR,PQ=6cm,PR=9cm and M is a point on QR such that it divides QR in the ratio 1:2PM⊥QR. Find QR.
View SolutionIn a ∠PQR, M lies on PR and between P and R such that QR=QM=PM. If ∠MQR=40∘, then find ∠P.
View SolutionPQR एक समकोण त्रिभुज है जिसका कोण P समकोण है तथा QR पर बिंदु M इस प्रकार स्थित है कि PM⊥QR है । दर्शाइए कि PM2=QM.MR है ।
View SolutionIn ΔPQR, seg PM is median. PM=9, PQ2+PR2=290 then find length of seg QR.
View SolutionIn the figure, ∠QPR=90∘, seg PM⊥ seg QR and Q−M−R, PM=10. QM=8, find QR.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM⊥QR . Show that PM2=QM.MR.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2=QM.MR .
View SolutionIn the adjoining figure, M is the midpoint of QR. anglePRQ = 90^(@) prove that PQ^(2) = 4 PM^(2) - 3 PR^(2)
View SolutionIn ΔPQR,∠PQR=90∘,segQM⊥hypPR,PM=16andRM=9thenQM…….
View SolutionDelta PQR is an "equilateral triangle", "seg" PM bot side QR, Q -M- R "Prove that" : PQ^(2) = 4QM^(2)
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2 = QM .MR.
View Solution
