Circles with different radii but same centre are called………………..Solution in Tamil
The correct Answer is:Concentric circles
Step by step video, text & image solution for Circles with different radii but same centre are called……………….. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Draw segment PQ=4.3cm and bisect it.
View SolutionSelect the appropriate alternative : In the adjoining figure ,PQ∣∣AC.BP=6,PA=8,BQ=9 , then QC = ……………

View SolutionChoose the correct alternative among the following :
The class mark of the class interval 120-130 is,
View SolutionTwo arcs of same length of two different circles subtended angles of 25^(@) and 75^(@) at their centres respectively.Then the ratio of the radii of the circles is
View SolutionCONCENTRIC CIRCLES Circles having the same centre but with different radii are said to be concentric circles.
View SolutionThe circle having the same center but with different radii is known as.
View Solutionवे सभी वृत्त जिनके केंद्र समान और विभिन्न त्रिज्याएँ हो, ………… वृत्त कहलाती हैं ।
View SolutionRecall that two circles are congruent, if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres
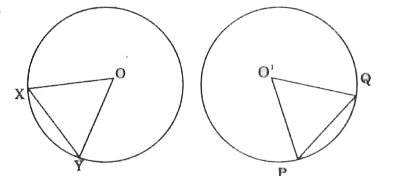
View SolutionCircles having the same centre and different radii are called____circles.
View SolutionTwo circle having same centre are called
View SolutionIf the circles of same radii and with centres (2,3),(5,6) cut orthogonally then radius is
View SolutionRecall that two circles are congruent if they have the same radii. Proe that equal chords of congruent circles subtend equal angles at their centres.
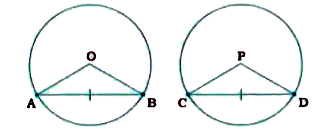
View SolutionTwo arcs of same length of two differen circles subtended angles of 25∘and75∘ at their centres respectively. Then the ratio of the radii of the circles is
View SolutionCircles with different radii but same centre are called……….
View SolutionName the circles having the same centre and different radii.
View Solution
