Circles with different radii but same centre are called……….Solution in Marathi
Step by step video & image solution for Circles with different radii but same centre are called………. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two circles of radii 5.5 cm and 3.3 cm respectively touch each other.What is the distance between their centres?
View SolutionRewrite the following statement in 'if-then' form. 'Diagonals of a parallelogram bisect each other.'
View SolutionSeg AB is parallel to Y-axis and co-ordinates of point A are (1,3), then co-ordinates of point B can be……….a) (3,1) b) (5,3) c) (3,0) d) (1,-3)
View SolutionTwo arcs of same length of two different circles subtended angles of 25^(@) and 75^(@) at their centres respectively.Then the ratio of the radii of the circles is
View SolutionCONCENTRIC CIRCLES Circles having the same centre but with different radii are said to be concentric circles.
View SolutionThe circle having the same center but with different radii is known as.
View Solutionवे सभी वृत्त जिनके केंद्र समान और विभिन्न त्रिज्याएँ हो, ………… वृत्त कहलाती हैं ।
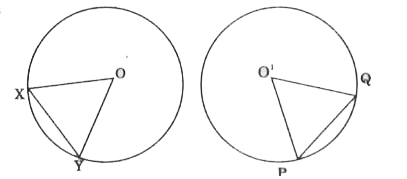
View SolutionRecall that two circles are congruent, if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres
View SolutionCircles having the same centre and different radii are called____circles.
View SolutionTwo circle having same centre are called
View SolutionCircles with different radii but same centre are called………………..
View SolutionIf the circles of same radii and with centres (2,3),(5,6) cut orthogonally then radius is
View SolutionRecall that two circles are congruent if they have the same radii. Proe that equal chords of congruent circles subtend equal angles at their centres.
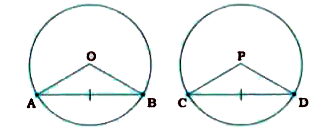
View SolutionTwo arcs of same length of two differen circles subtended angles of 25∘and75∘ at their centres respectively. Then the ratio of the radii of the circles is
View SolutionName the circles having the same centre and different radii.
View Solution