A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
To find the height of the platform formed by the earth dug out from a well, we will follow these steps:
Step 1: Calculate the volume of the well
The volume V of a cylindrical well can be calculated using the formula:
V=πr2h
where:
- r is the radius of the well,
- h is the height (or depth) of the well.
Given:
- Diameter of the well = 7 m, so the radius r=72=3.5 m.
- Depth of the well h=20 m.
Now substituting the values into the formula:
V=π(3.5)2×20
=π×12.25×20
=π×245
Using π≈227:
V=227×245
Calculating this gives:
=22×35=770 m3
Step 2: Calculate the volume of the platform
The volume Vp of the platform, which is a rectangular prism (cuboid), can be calculated using the formula:
Vp=l×b×h
where:
- l is the length of the platform,
- b is the breadth of the platform,
- h is the height of the platform (which we need to find).
Given:
- Length l=22 m,
- Breadth b=14 m,
- Height h=?.
So we have:
Vp=22×14×h
=308h m3
Step 3: Set the volumes equal to each other
Since the volume of the earth dug out from the well is equal to the volume of the platform, we can set the two volumes equal:
770=308h
Step 4: Solve for h
To find h, we rearrange the equation:
h=770308
Calculating this gives:
h=2.5 m
Conclusion
The height of the platform is 2.5 meters.
---
The volume V of a cylindrical well can be calculated using the formula:
V=πr2h
where:
- r is the radius of the well,
- h is the height (or depth) of the well.
- Diameter of the well = 7 m, so the radius r=72=3.5 m.
- Depth of the well h=20 m.
V=π(3.5)2×20
=π×12.25×20
=π×245
Using π≈227:
V=227×245
Calculating this gives:
=22×35=770 m3
The volume Vp of the platform, which is a rectangular prism (cuboid), can be calculated using the formula:
Vp=l×b×h
where:
- l is the length of the platform,
- b is the breadth of the platform,
- h is the height of the platform (which we need to find).
- Length l=22 m,
- Breadth b=14 m,
- Height h=?.
Vp=22×14×h
=308h m3
Since the volume of the earth dug out from the well is equal to the volume of the platform, we can set the two volumes equal:
770=308h
To find h, we rearrange the equation:
h=770308
Calculating this gives:
h=2.5 m
The height of the platform is 2.5 meters.
Topper's Solved these Questions
- SURFACE AREAS AND VOLUMESBook:NCERTChapter:SURFACE AREAS AND VOLUMESExercise:Solved Examples
Explore 14 Videos
- SURFACE AREAS AND VOLUMESBook:NCERTChapter:SURFACE AREAS AND VOLUMESExercise:EXERCISE 13.5
Explore 7 Videos
- SURFACE AREAS AND VOLUMESBook:NCERTChapter:SURFACE AREAS AND VOLUMESExercise:Exercise 13.4
Explore 5 Videos
- STATISTICSBook:NCERTChapter:STATISTICSExercise:EXERCISE 14.1
Explore 9 Videos
- TRIANGLESBook:NCERTChapter:TRIANGLESExercise:SOLVED EXAMPLES
Explore 14 Videos
Similar Questions
Selvis house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57m×1.44m×95cm. The overhead tank has its radius 60 cm and height 95 cm. Find the height of the water left in the underground tank after the overhead tank has been completely filled with water from underground tank which had been full. Compare the capacity of both the tanks. (take π = 22/7)
View SolutionDerive the formula for the curved surface area and total surface area of the frustum of a cone.
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
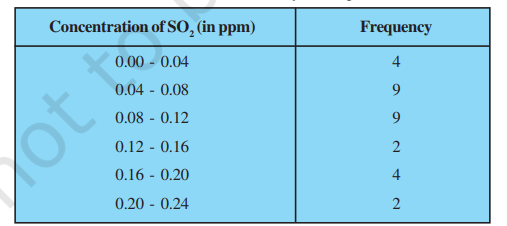
View SolutionTo find out the concentration of SO2in the air (in parts per million, i.e., ppm), the data was collected for 30 localities in a certain city and is presented below:Find the mean concentration of SO2in the air.
View SolutionIn figure∠ACB=90∘and CD⊥AB. Prove that BC2AC2=BDAD.
View SolutionA 16 m deep well with diameter 3.5 m is dug up and the earth from it is spread evenly to form a platform 27.5 m by 7 m. Find the height of the platform.
View Solutionव्यास 7 मीटर वाला 20 मीटर गहरा एक कुँआ खोदा जाता है और खोदने से निकली हुई मिट्टी को समान रूप में फैलाकर 22 मी. × 14 मी. वाला एक चबूतरा बनाया गया है | इस चबूतरा बनाया गया है | इस चबूतरे की ऊँचाई ज्ञात कीजिए |
View SolutionA 21-m-deep well with diameter 6 m is dug and the earth from digging is evenly spead to form a platform 27m×11 m. Find the height of the platfrom.
View Solution7 मी व्यास वाला 20 मी गहरा कुआँ खोदा जाता है और खोदने से निकली हुई मिट्टी को समान रूप से फैला कर 22 मी ×14 मी वाला चबूतरा बनाया जाता है। इस चबूतरे की ऊँचाई ज्ञात कीजिए।
View Solutionएक 2 मीटर व्यास का कुआँ 14 मी. गहराई तक खोदा गया है। कुएँ से निकली मिट्टी को इसके चारों ओर समान रूप से बिछाकर एक 40 सेमी. ऊँचाई का चबूतरा बनाया जाता है। चबूतरे की चौड़ाई ज्ञात कीजिए।
View Solutionव्यास 7 मी वाला 20 मी गहरा एक कुआँ खोदा जाता है, और खोदने से निकली हुए मिट्टी को समान रूप से फैलाकर 22 मी ×14 मी वाला एक चबूतरा बनाया गया है । इस चबूतरे की ऊंचाई ज्ञात कीजिए ।
View SolutionA 20 m deep well with diameter 7 m. is dug and the earth got by digging is evenly spread out to form a rectangular platform of base 22m. × 14m. Find the height of the platform.
View SolutionA 20 m deep well with diameter 7 m. is dug and the earth got by digging is evenly spread out to form a rectangular platform of base 22m. × 14m. Find the height of the platform.
View SolutionA 20m deep well of diameter 7 m is dug and the earth got by digging is evenly spread out to form a rectangular platform of base 22 m × 14 m. Find the height of the platform.
View SolutionA 20m deep well of diameter 7 m is dug and the earth got by digging is evenly spread out to form a rectangular platform of base 22 m × 14 m. Find the height of the platform.
View SolutionA 20m deep well of diameter 7 m is dug and the earth got by digging is evenly spread out to form a rectangular platform of base 22 m × 14 m. Find the height of the platform.
View Solution
