In figure∠ACB=90∘and CD⊥AB. Prove that BC2AC2=BDAD.
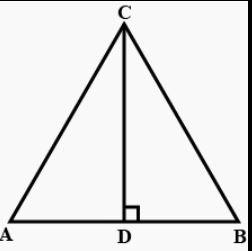
In triangles ACD and ABC, we have,
∠ADC=∠ACB [Each equal to 90∘ ]
and, ∠DAC=∠BAC [Common]
So, by AA-criterion of similarity, we have
△ACD∼△ABC
⇒ACAB=ADAC
⇒AC2=AB×AD......(i)
In △BCD and △BAC, we have
∠BDC=∠BCA
∠DBC=∠ABC
So, by AA-criterion of similarity, we have
△BCD∼△BAC
⇒BCBD=BABC
⇒BC2=AB×BD......(ii)
Dividing (ii) by (i), we get
((BC)2(AC)2)=AB×BDAB×AD
⇒(BC)2(AC)2=BDAD
[Hence proved]
Topper's Solved these Questions
Similar Questions
In figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
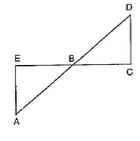
View SolutionIn Figure, ∠E>∠A and ∠C>∠D . Prove that AD>EC
 View Solution
View SolutionIn ABC, ∠A=60o . Prove that B C^2=A B^2+A C^2-A B.A C .
View SolutionIn figure D is a point on side BC of a ΔABCsuch that BDCD=ABAC. Prove that AD is the bisector of ∠BAC.
 View Solution
View SolutionIn the given figure, ∠B<∠Aand∠C<∠D. Show that AD<BC.
View SolutionIn ABC , ∠A is obtuse, PB⊥AC and QC⊥AB . Prove that: AB×AQ=AC×AP (ii) BC2=(AC×CP+AB×BQ)
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD
 View Solution
View SolutionIn fig., D is a point on hypotenuse AC of ΔABC,DM⊥BCand DN⊥AB. Prove that
(i) DM2=DN⋅MC
(ii) DN2=DM⋅AN
 View Solution
View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
View Solution

