An inclined plane making an angle β with horizontal. A projectile projected from the bottom of the plane with a speed u at angle α with horizontal, then its maximum range Rmax is
Rmax=u2g(1−sinβ)
Rmax=u2g(1+sinβ)
Rmax=u2g(1−sinβ)
Rmax=u2g(1+sinβ)
The correct Answer is:B
To find the maximum range Rmax of a projectile launched from the bottom of an inclined plane at an angle α with respect to the horizontal, we can follow these steps:
Step 1: Define the Coordinate System
We set up a coordinate system where the x-axis is along the inclined plane and the y-axis is perpendicular to it. The inclined plane makes an angle β with the horizontal.
Step 2: Resolve the Initial Velocity
The initial velocity u can be resolved into two components:
- Along the incline (x-direction):
ux=ucos(α−β)
- Perpendicular to the incline (y-direction):
uy=usin(α−β)
Step 3: Analyze the Motion in the y-direction
The vertical motion is influenced by gravity. The acceleration due to gravity acting downwards can be resolved into two components:
- Perpendicular to the incline:
gy=gcosβ
- Along the incline:
gx=gsinβ
Since the projectile returns to the same vertical level, we can set up the equation for vertical displacement:
0=uyt−12gyt2
Substituting uy:
0=(usin(α−β))t−12gcosβt2
Step 4: Solve for Time of Flight
Factoring out t gives:
t(usin(α−β)−12gcosβt)=0
The non-trivial solution gives:
t=2usin(α−β)gcosβ
Step 5: Analyze the Motion in the x-direction
The horizontal displacement (range R) can be expressed as:
R=uxt
Substituting ux and t:
R=(ucos(α−β))(2usin(α−β)gcosβ)
This simplifies to:
R=2u2sin(α−β)cos(α−β)gcosβ
Step 6: Use Trigonometric Identity
Using the identity 2sinAcosA=sin(2A):
R=u2sin(2(α−β))gcosβ
Step 7: Maximize the Range
To maximize R, we need to maximize sin(2(α−β)). The maximum value of sine is 1, which occurs when:
2(α−β)=π2⟹α−β=π4
Thus, the maximum range Rmax becomes:
Rmax=u2gcos2β(1−sinβ)
Step 8: Final Expression for Maximum Range
After simplification, we find:
Rmax=u2g(1+sinβ)
Conclusion
The maximum range Rmax of the projectile launched from the bottom of the inclined plane is given by:
Rmax=u2g(1+sinβ)
We set up a coordinate system where the x-axis is along the inclined plane and the y-axis is perpendicular to it. The inclined plane makes an angle β with the horizontal.
The initial velocity u can be resolved into two components:
- Along the incline (x-direction):
ux=ucos(α−β)
- Perpendicular to the incline (y-direction):
uy=usin(α−β)
The vertical motion is influenced by gravity. The acceleration due to gravity acting downwards can be resolved into two components:
- Perpendicular to the incline:
gy=gcosβ
- Along the incline:
gx=gsinβ
0=uyt−12gyt2
Substituting uy:
0=(usin(α−β))t−12gcosβt2
Factoring out t gives:
t(usin(α−β)−12gcosβt)=0
The non-trivial solution gives:
t=2usin(α−β)gcosβ
The horizontal displacement (range R) can be expressed as:
R=uxt
Substituting ux and t:
R=(ucos(α−β))(2usin(α−β)gcosβ)
This simplifies to:
R=2u2sin(α−β)cos(α−β)gcosβ
Using the identity 2sinAcosA=sin(2A):
R=u2sin(2(α−β))gcosβ
To maximize R, we need to maximize sin(2(α−β)). The maximum value of sine is 1, which occurs when:
2(α−β)=π2⟹α−β=π4
Thus, the maximum range Rmax becomes:
Rmax=u2gcos2β(1−sinβ)
After simplification, we find:
Rmax=u2g(1+sinβ)
The maximum range Rmax of the projectile launched from the bottom of the inclined plane is given by:
Rmax=u2g(1+sinβ)
Topper's Solved these Questions
Similar Questions
An inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
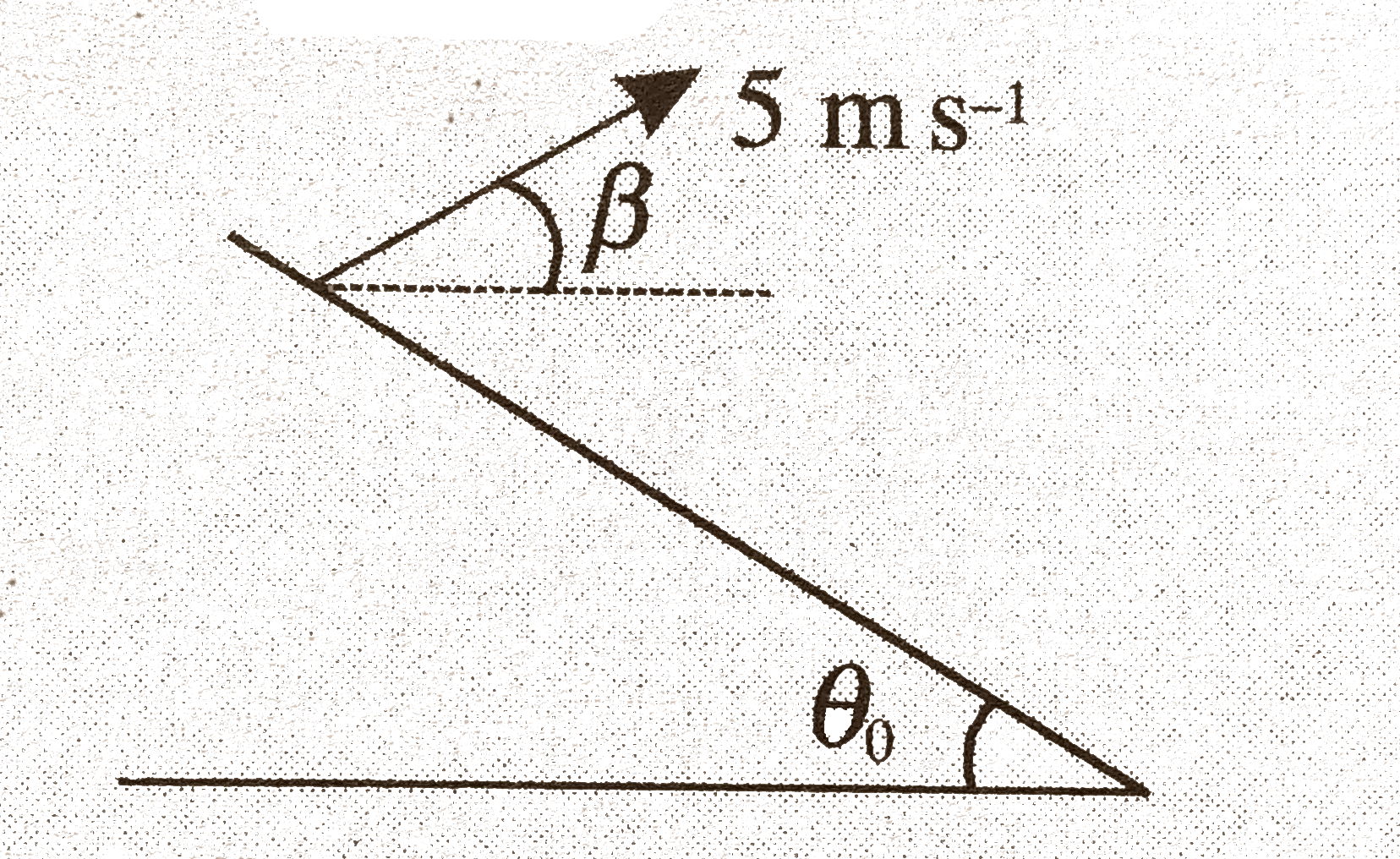 .
.
View SolutionA projectile is projected with velocity u making angle θ with horizontal direction, find : horizontal range.
View Solution
Knowledge Check
An inclined plane makes an angle of 60∘ with horizontal. A disc rolling acceleration equal to:
Ag3B34gCg√3Dg2A plane surface is inclined making an angle β above the horizon. A bullet is fired with the point of projection at the bottom of the inclined plane with velocity u, then the maximum range is given by:
Au2gBu2g(1+sinβ)Cu2g(1−sinβ)Du2g(1+cosβ)A body is projected up along an inclined plane from the bottom with speed is 2v.If it reaches the bottom of the plane with a velocity v,if θ is the angle of inclination with the horizontal and μ be the coefficient of friction.
A53tanθB35tanθC15tanθD25tanθ
A projectile is fired with a speed u at an angle θ with the horizontal. Find its speed when its direcrtion of motion makes an angle α with the horizontal.
View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA particle is thrown with speed u at an angle α with horizontal from the ground. After how much time, the velocity of particle will make an angle β with horizontal.
View SolutionParticle "A" is released from a point "P" on a smooth inclined plane inclined at an angle α with the horizontal.At the same instant another particle "B" is projected with initial velocity 'u' making an angle β 'with the horizontal.Both the particles meet again on the inclined plane.the relation between ' α and β is 1) α+β=π6 2) α+β=π4 3) α+β=π3 4) α+β=π2
View SolutionA body is projected with a speed (u) at an angle to the horizontal to have maximum range. What is its velocity at the highest point ?
View Solution
