For pair production i.e. for the production of electron and positron, the incident photon must have a minimum frequency of the order of
1018s−1
1021s−1
1025s−1
1030s−1
The correct Answer is:B
To solve the problem of determining the minimum frequency of a photon required for pair production of an electron and a positron, we can follow these steps:
Step 1: Understand Pair Production
Pair production occurs when a photon interacts with a strong electromagnetic field (usually near a nucleus) to produce a particle-antiparticle pair, such as an electron and a positron. The energy of the photon must be sufficient to create these particles.
Step 2: Calculate the Rest Mass Energy
The rest mass energy (E) of a particle is given by the equation:
E=mc2
where:
- m is the mass of the particle,
- c is the speed of light (c≈3×108m/s).
For an electron and a positron:
- Mass of an electron (me) = 9.11×10−31kg
- Mass of a positron (mp) = 9.11×10−31kg
The total rest mass energy for the electron-positron pair is:
Etotal=2×mec2
Step 3: Convert Mass to Energy in MeV
Using the conversion factor 1kg=6.242×1012MeV:
Etotal=2×(9.11×10−31kg)×(3×108m/s)2
Calculating this gives:
Etotal≈2×0.511MeV=1.022MeV
Step 4: Relate Energy to Frequency
The energy of a photon is also related to its frequency (f) by the equation:
E=hf
where h is Planck's constant (h≈6.626×10−34Js).
Step 5: Calculate Minimum Frequency
Setting the energy equal to the photon energy, we have:
hf=1.022MeV
To find the frequency:
f=Eh=1.022×106eV6.626×10−34Js
Step 6: Convert MeV to Joules
Using the conversion 1eV=1.6×10−19J:
1.022MeV=1.022×106×1.6×10−19J
Step 7: Substitute and Calculate
Substituting this back into the frequency equation:
f=1.022×106×1.6×10−196.626×10−34
Step 8: Final Calculation
Calculating this gives:
f≈2.5×1020Hz
Conclusion
The minimum frequency of the incident photon required for pair production of an electron and positron is of the order of 1020Hz.
Pair production occurs when a photon interacts with a strong electromagnetic field (usually near a nucleus) to produce a particle-antiparticle pair, such as an electron and a positron. The energy of the photon must be sufficient to create these particles.
The rest mass energy (E) of a particle is given by the equation:
E=mc2
where:
- m is the mass of the particle,
- c is the speed of light (c≈3×108m/s).
- Mass of an electron (me) = 9.11×10−31kg
- Mass of a positron (mp) = 9.11×10−31kg
Etotal=2×mec2
Using the conversion factor 1kg=6.242×1012MeV:
Etotal=2×(9.11×10−31kg)×(3×108m/s)2
Calculating this gives:
Etotal≈2×0.511MeV=1.022MeV
The energy of a photon is also related to its frequency (f) by the equation:
E=hf
where h is Planck's constant (h≈6.626×10−34Js).
Setting the energy equal to the photon energy, we have:
hf=1.022MeV
To find the frequency:
f=Eh=1.022×106eV6.626×10−34Js
Using the conversion 1eV=1.6×10−19J:
1.022MeV=1.022×106×1.6×10−19J
Substituting this back into the frequency equation:
f=1.022×106×1.6×10−196.626×10−34
Calculating this gives:
f≈2.5×1020Hz
The minimum frequency of the incident photon required for pair production of an electron and positron is of the order of 1020Hz.
Topper's Solved these Questions
Similar Questions
(a) The rest mass energy of an electron is m0c2=0.51MeV. Can a photon of this energy create an electron in free space?
(A) A single photon of energy 2m0c2 or greater has enough energy to form an electron (e−). Positron (e+) pair. But prove that this process cannot occur in free space.
(c) The pair production is possibel in presence of a third particle. Assume that a photon having frequency v collides with a nucleus of rest mass M0 (at rest) and creates an e−,e+ pair at rest. Calculate the mass M0 of the nucleus.
Neglect relativistic effect in all questions.
View SolutionWork function for potassium is 2.0 eV. For photoelectric emision from a potassium surface the minimum frequency of incident radiation must be _____.
View Solution
Knowledge Check
For pair production i.e. for the production of electron and positron, the incident photon must have a minimum frequency of the order of
A1018s−1B1021s−1C1025s−1D1030s−1To produce an electron-position pair, the minimum energy of γ-ray photon must be
A1.02keVB1.02MeVC1.02BeVD1.02eVFor production of beats the two souces must have
Adiffernet frequencies and saem ampltudeBdifferent frequenciesCifferent frequencies, same amplitude and same phaseDdifferent frequencies and same phase
What is the minimum product of the uncrtainty in position and the uncertainty in momentum of a miving electron ?
View SolutionIs it necessary for production of beats that the two waves must have exactly equal amplitudes?
View SolutionExplain how Einstein's photoelectric equation enables us to understand the (i) linear dependence, of the maximum K.E. of the emitted electrons, on the frequency of the incident radiations (ii) existance of a threshold frequency for a given photoemitter.
View SolutionIn NO−3 ion, the number of bond pairs and lone pairs of electrons on nitrogen atom are
Thinking process
To solve this sequence we must know the structure of NO−3 ion i.e,
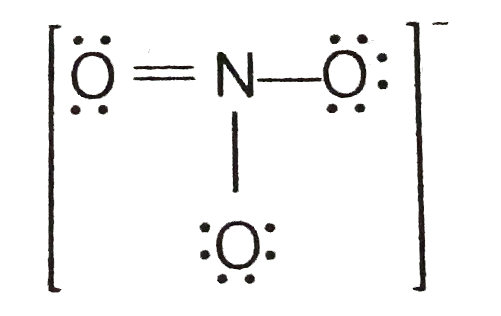
Then, cound the bond pairs and lone pairs of electron on nitrogen.
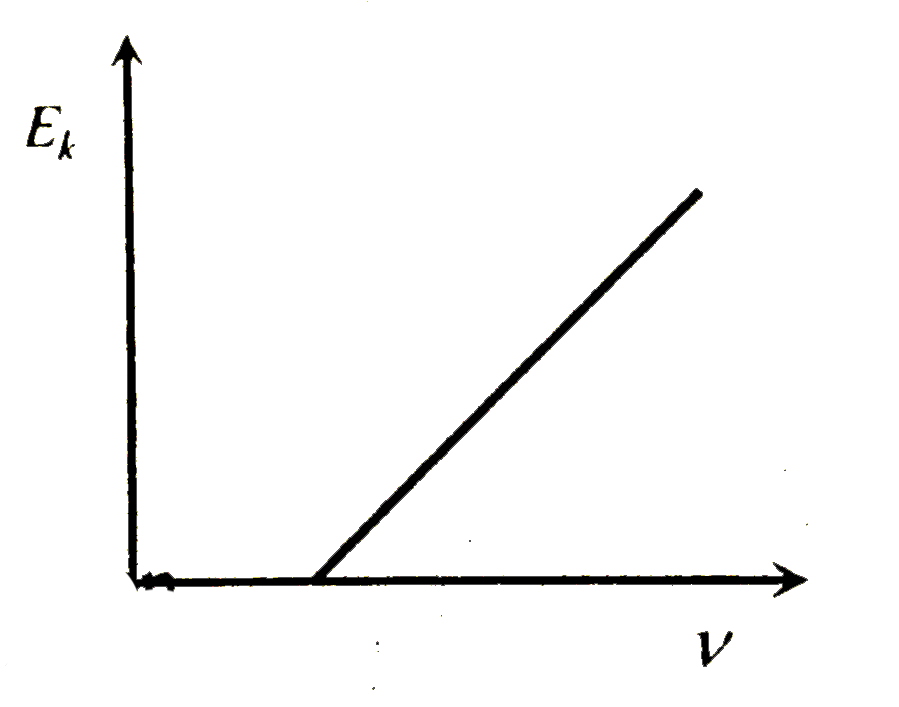
View SolutionFor the photoelectric effect, the maximum kinetic energy Ek of the emitted photoelectrons is plotted against the frequency of the incident photons as shown in the figure. The slope of the curve gives
View Solution
