Explain how Einstein's photoelectric equation enables us to understand the (i) linear dependence, of the maximum K.E. of the emitted electrons, on the frequency of the incident radiations (ii) existance of a threshold frequency for a given photoemitter.
To understand how Einstein's photoelectric equation provides insights into the linear dependence of the maximum kinetic energy of emitted electrons on the frequency of incident radiation and the existence of a threshold frequency, we can break down the explanation into two parts.
1. Einstein's Photoelectric Equation:
The photoelectric equation is given by:
KEmax=hν−ν0
where:
- KEmax is the maximum kinetic energy of the emitted electrons,
- h is Planck's constant,
- ν is the frequency of the incident radiation,
- ν0 is the threshold frequency (the minimum frequency required to emit electrons).
2. Linear Dependence of Maximum K.E. on Frequency:
From the equation, we can see that the maximum kinetic energy KEmax is directly proportional to the frequency ν of the incident radiation. This can be rearranged to show:
KEmax=hν−ν0
This equation resembles the equation of a straight line y=mx+c, where:
- y corresponds to KEmax,
- x corresponds to ν,
- m (the slope) is equal to h,
- c (the y-intercept) is equal to −ν0.
Thus, as the frequency ν increases, the maximum kinetic energy KEmax increases linearly, confirming the linear dependence.
3. Existence of Threshold Frequency:
The threshold frequency ν0 is the minimum frequency required to emit electrons. If the frequency of the incident radiation is less than ν0, we can analyze the equation:
KEmax=hν−ν0
If ν<ν0, then:
KEmax<0
A negative kinetic energy does not have a physical meaning, as kinetic energy cannot be negative. Therefore, for electrons to be emitted, the frequency of the incident radiation must be at least equal to the threshold frequency ν0. If the frequency is lower than this threshold, no electrons will be emitted, and the photoelectric effect will not occur.
Summary:
- The linear dependence of maximum kinetic energy on frequency is derived from the direct proportionality in Einstein's photoelectric equation.
- The existence of a threshold frequency is explained by the requirement that the frequency must be equal to or greater than ν0 to avoid negative kinetic energy.
The photoelectric equation is given by:
KEmax=hν−ν0
where:
- KEmax is the maximum kinetic energy of the emitted electrons,
- h is Planck's constant,
- ν is the frequency of the incident radiation,
- ν0 is the threshold frequency (the minimum frequency required to emit electrons).
From the equation, we can see that the maximum kinetic energy KEmax is directly proportional to the frequency ν of the incident radiation. This can be rearranged to show:
KEmax=hν−ν0
This equation resembles the equation of a straight line y=mx+c, where:
- y corresponds to KEmax,
- x corresponds to ν,
- m (the slope) is equal to h,
- c (the y-intercept) is equal to −ν0.
The threshold frequency ν0 is the minimum frequency required to emit electrons. If the frequency of the incident radiation is less than ν0, we can analyze the equation:
KEmax=hν−ν0
If ν<ν0, then:
KEmax<0
A negative kinetic energy does not have a physical meaning, as kinetic energy cannot be negative. Therefore, for electrons to be emitted, the frequency of the incident radiation must be at least equal to the threshold frequency ν0. If the frequency is lower than this threshold, no electrons will be emitted, and the photoelectric effect will not occur.
- The linear dependence of maximum kinetic energy on frequency is derived from the direct proportionality in Einstein's photoelectric equation.
- The existence of a threshold frequency is explained by the requirement that the frequency must be equal to or greater than ν0 to avoid negative kinetic energy.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - NCERT Exerciese question1videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Short answer1videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Problems for Practice (B)2videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Multiple Choice Questions1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
What is photoelectric effect? Give any two practical applications of this effect. Write Einstein's photoelectric equation and use it to explain (i) independence of maximum energy of the emitted photoelectrons from intensity of incident light (ii) existence of a threshold frequency of the emitted photoelectrons from intensity of incident light.
View SolutionDoes the 'stopping potential' in photoelectric emission depend upon
(i) the intensity of the incident radiation in a photocell. ?
(ii) The frequency of the incident radiation ?View Solution
Knowledge Check
- Question 1 - Select One
According to Einstein's photoelectric equation, the plot of the maximum kinetic energy of the emitted photoelectrons from a metal versus frequency of the incident radiation gives a straight line whose slope
Adepends on the nature of metal usedBdepends on the intensity or radiationCdepends on both intensity of radiation and the nature of metal usedDis the same for all metals and independent of the instensity or radiation - Question 2 - Select One
Maximum kinetic energy (Ek) of a photoelectron varies with the frequency (v) of the incident radiation as
A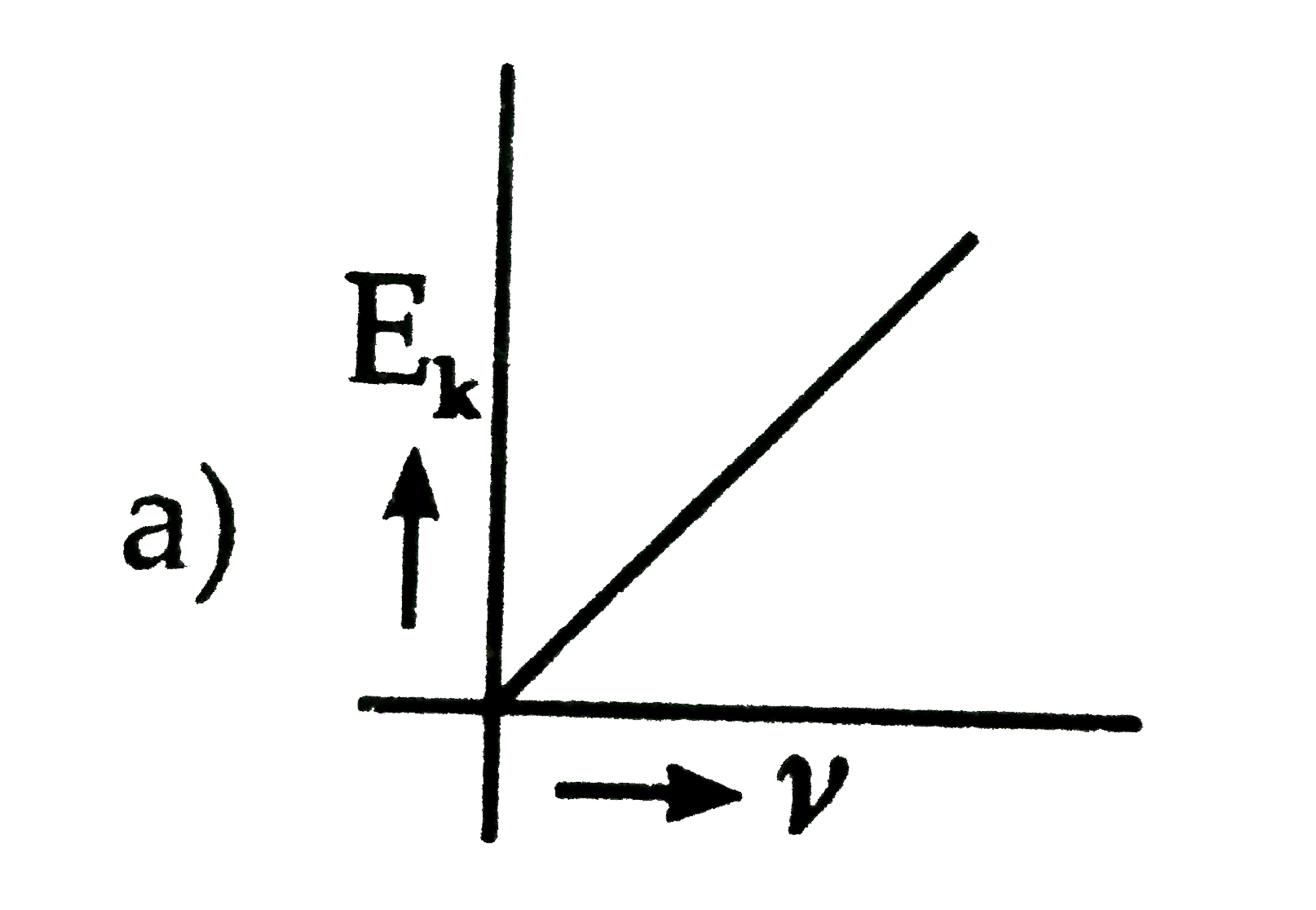 B
B C
C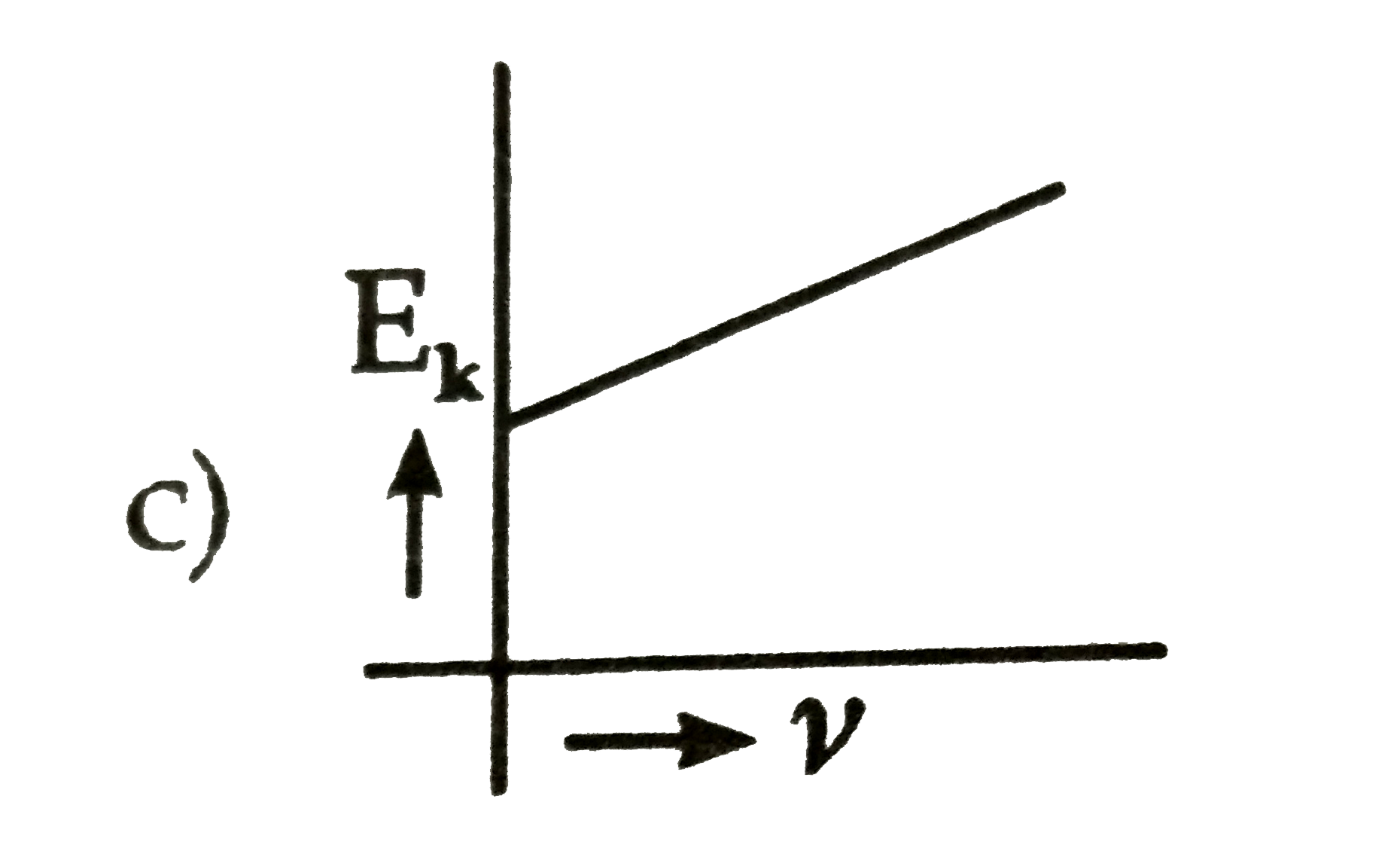 D
D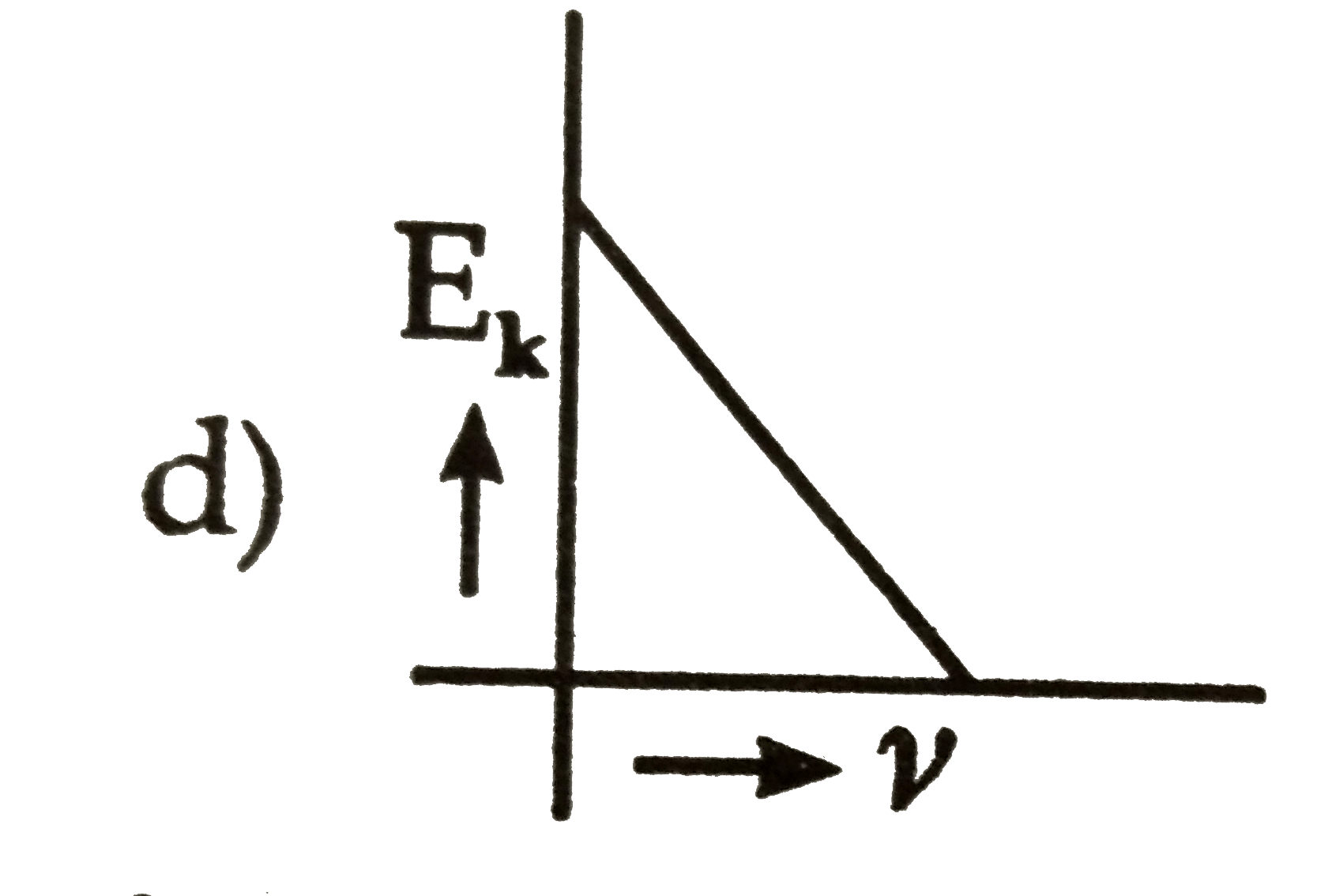
- Question 3 - Select One
According to Einstein's photoelectric equation, the graph between the kinetic energy of photoelectrons ejected and the frequency of incident radiation is
A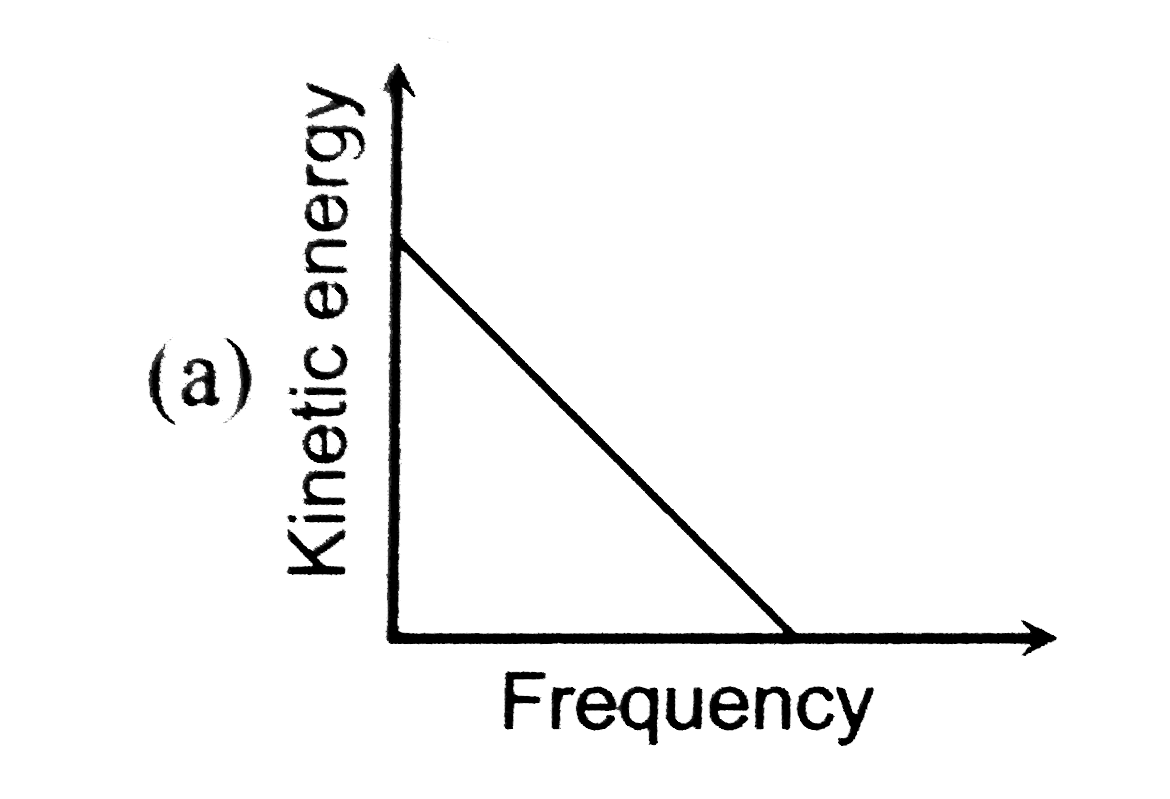 B
B C
C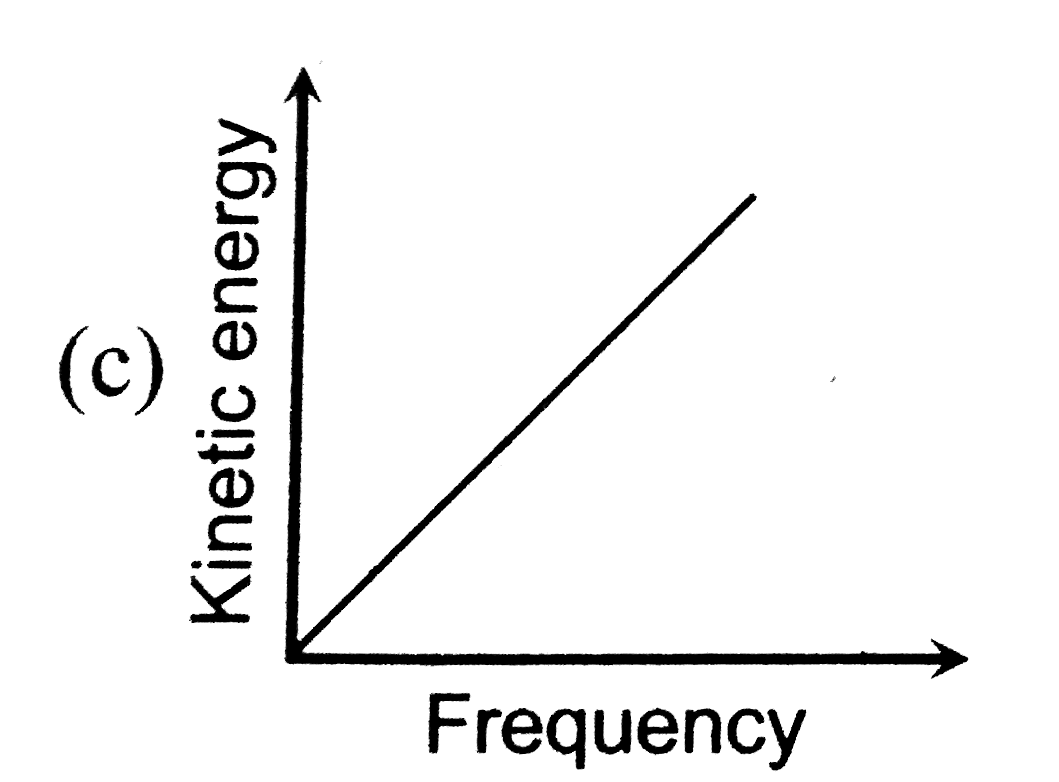 D
D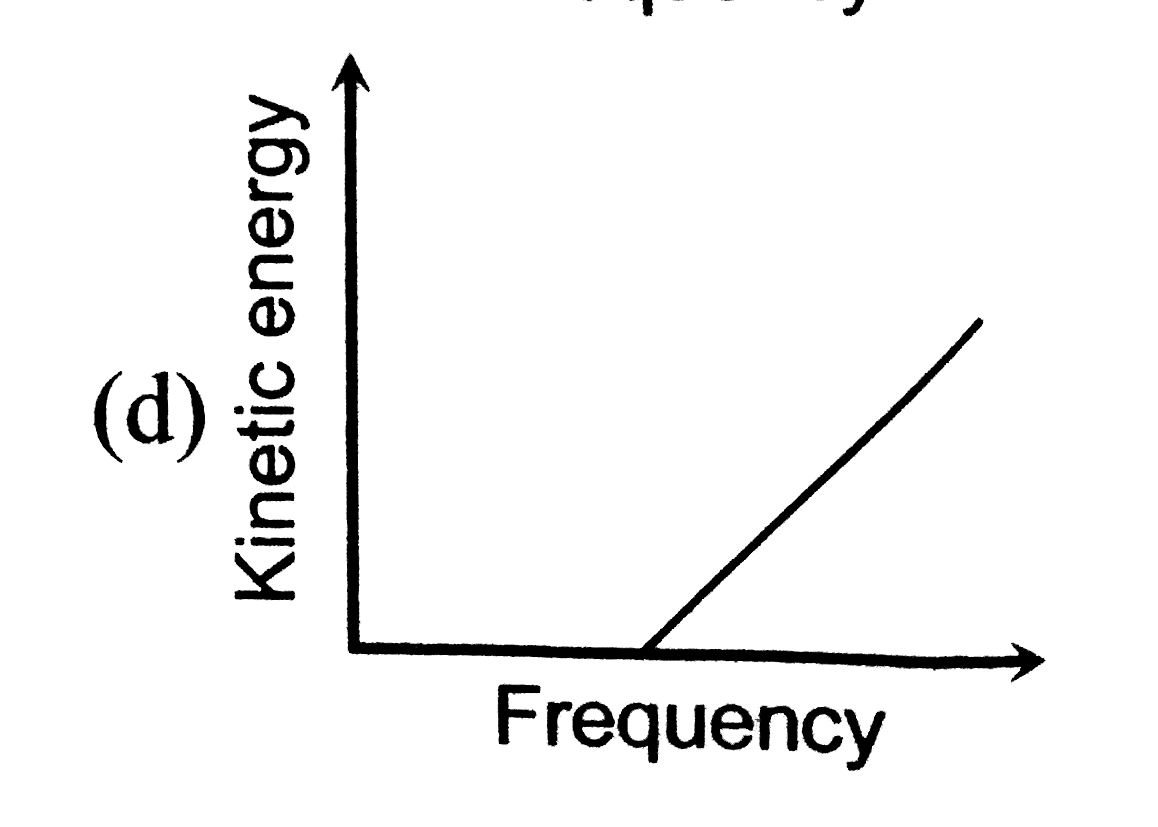
According to Einstein's photoelectric equation, the graph between kinetic energy of photoelectrons ejected and the frequency of the incident radiation is :
View SolutionDerive de Broglie wave equation for material particles.
(b) Why does photoelectric emission not take place if the frequency of incident radiation is less than threshold frequency ?View SolutionWrite Einsteins's photoelectric equation. Explain the terms (i) threshold frequency, and (ii) stopping potential.
View SolutionFor the photoelectric effect, the maximum kinetic energy Ek of the emitted photoelectrons is plotted against the frequency ν of the incident photons as shown in the figure. The slope of the curve gives
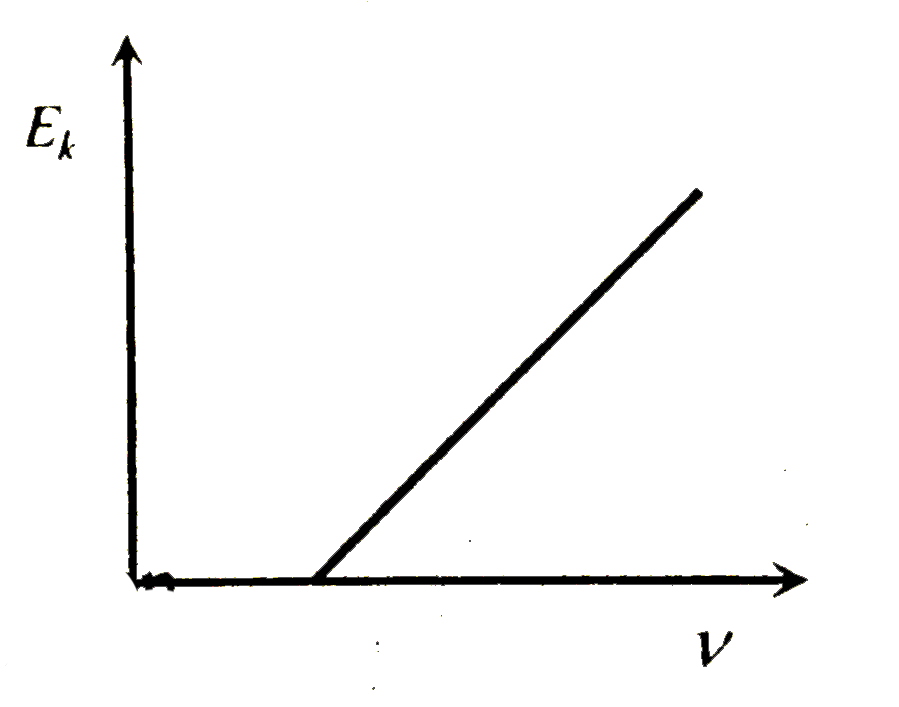 View Solution
View SolutionFor the photoelectric effect, the maximum kinetic energy Ek of the emitted photoelectrons is plotted against the frequency of the incident photons as shown in the figure. The slope of the curve gives
 View Solution
View Solution

