A line $L_{1} \equiv 3 y - 2 x - 6 = 0$ is rotated about its point of intersection with the y-axis in the clockwise direction to make it $L_{2}$ such that the are formed by $L_{1}, L_{2}$ the x-axis, and line $x = 5$ is $\frac{49}{3} s q . u n i t s$ if its point of intersection with $x = 5$ lies below the x-axis. Find the equation of $L_{2} .$

Video Solution

Answer

Step by step video & image solution for A line L_1-=3y-2x-6=0 is rotated about its point of intersection with the y-axis in the clockwise direction to make it L_2 such that the are formed by L_1,L_2 the x-axis, and line x=5 is (49)/3s qdotu n i t s if its point of intersection with x=5 lies below the x-axis. Find the equation of L_2dot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS STRAIGHT LINES

Knowledge Check

Question 1 - Select One
The area of triangle formed by the lines $l_{1} and l_{2}$ and the x-axis is:

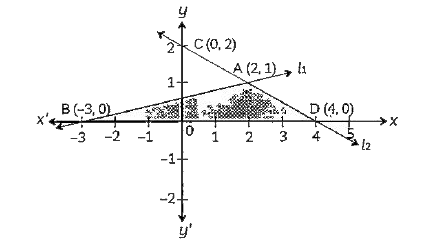A7 sq. units
B $\frac{9}{2}$ sq.units
C $\frac{7}{2}$ sq.units
D4 sq. units
Question 2 - Select One
Find 14.28% of 49 =?
Aa. 8
Bb. 11
Cc. 7
Dd. 16
Question 3 - Select One
Lying in the plane $x + y + z = 6$ is a line L passing through (1, 2, 3) and perpendicular to the line of intersection of planes $x + y + z = 6$ and $2 x - y + z = 4$ , then the equation of L is
A $\frac{x - 1}{4} = \frac{y - 2}{- 7} = \frac{z - 3}{3}$
B $\frac{x - 1}{2} \frac{y - 2}{1} = \frac{z - 3}{- 3}$
C $\frac{x - 1}{4} = \frac{y - 2}{- 5} = \frac{z - 3}{1}$
D $\frac{x - 1}{3} = \frac{y - 2}{1} = \frac{z - 3}{- 4}$

Similar Questions

Knowledge Check

The area of triangle formed by the lines $l_{1} and l_{2}$ and the x-axis is:

Find 14.28% of 49 =?

Lying in the plane $x + y + z = 6$ is a line L passing through (1, 2, 3) and perpendicular to the line of intersection of planes $x + y + z = 6$ and $2 x - y + z = 4$ , then the equation of L is

Recommended Questions

A line L1≡3y−2x−6=0 is rotated about its point of intersection with the y-axis in the clockwise direction to make it L2 such that the are formed by L1,L2 the x-axis, and line x=5 is 493sq.units if its point of intersection with x=5 lies below the x-axis. Find the equation of L2.

Similar Questions

Knowledge Check

The area of triangle formed by the lines l1andl2 and the x-axis is:

Find 14.28% of 49 =?

Lying in the plane x+y+z=6 is a line L passing through (1, 2, 3) and perpendicular to the line of intersection of planes x+y+z=6 and 2x−y+z=4, then the equation of L is

Recommended Questions

The area of triangle formed by the lines $l_{1} and l_{2}$ and the x-axis is:

Lying in the plane $x + y + z = 6$ is a line L passing through (1, 2, 3) and perpendicular to the line of intersection of planes $x + y + z = 6$ and $2 x - y + z = 4$ , then the equation of L is