θ1andθ2 are the inclination of lines L1andL2 with the x-axis. If L1andL2 pass through P(x1,y1), then the equation of one of the angle bisector of these lines is
x−x1cos(θ1+θ22)=y−y1sin(θ1+θ22)
x−x1-sin(θ1−θ22)=y−y1cos(θ1−θ22)
x−x1sin(θ1+θ22)=y−y1cos(θ1+θ22)
x−x1-sin(θ1+θ22)=y−y1cos(θ1+θ22)
The correct Answer is:A, D

From the figure, angle bisectors B1 and B2 have inclinations of
θ1+θ22 and (π2+θ1+θ22) with the x-axis.
Therefore, equations of angle bisectors are
x−x1cos(θ1+θ22)=y−y1sin(θ1+θ22)
and x−x1cos(π2+θ1+θ22)=y−y1sin(π2+θ1+θ22)
or x−x1-sin(θ1+θ22)=y−y1cos(θ1+θ22)
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)
27 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MATRIX MATCH TYPE)
8 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (SINGLE CORRECT ANSWER TYPE)
82 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
θ1 and θ2 are the inclination of lines L1andL2 with the x-axis. If L1andL2 pass through P(x1,y1) , then the equation of one of the angle bisector of these lines is
(a) x−x1cos(θ1−θ22)=y−y1sin(θ1−θ22) (b)x−x1−sin(θ1−θ22)=y−y1cos(θ1−θ22) (c)x−x1sin(θ1−θ22)=y−y1cos(θ1−θ22) (d)x−x1−sin(θ1+θ22)=y−y1cos(θ1+θ22)
View SolutionThe equations of bisectors of two lines L1&L2 are 2x−16y−5=0 and 64x+8y+35=0. lf the line L1 passes through (−11,4), the equation of acute angle bisector of L1 & L2 is:
View SolutionGiven equation of line L1 is y=4

Find the equation of L2.
View SolutionGiven equation of line L1 is y=4
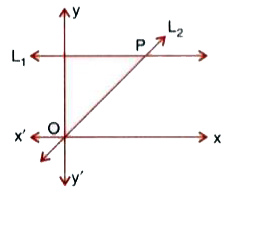
Write the slope of line L1 if L2 is the bisector of angle O.
View SolutionThe bisector of two lines L and L are given by 3x2−8xy−3y2+10x+20y−25=0. If the line L1 passes through origin, find the equation of line L2.
View SolutionA straight line L through the point (3,-2) is inclined at an angle 60∘ to the line √3x+y=1 If L also intersects the x-axis then the equation of L is
View SolutionGiven equation of line L1 is y = 4 and line L2 is the bisector of angle O.
Write the coordinates of point P.

View SolutionThe equation of line l1 is y=2x+3, and the equation of line l2 is y=2x-5.
View SolutionLet a given line L1 intersect the X and Y axes at P and Q respectively. Let another line L2 perpendicular to L1 cut the X and Y-axes at Rand S, respectively. Show that the locus of the point of intersection of the line PS and QR is a circle passing through the origin
View SolutionLet the straight lines x+y−2=0,2x−y+1=0andpx+qy−r=0 be concurrent and l1andl2 be the two members of the family of lines 2px+2qy+4r=0 which are nearest and farthest from origin : Now answer the question : The angle between lines L1andl2 is : (A) 450 (B) 600 (C) 900 (D) none of these
View Solution
