For the integer n , if n3 is odd, then which of the following statements are true? n is odd. II. n2 is odd. III. n2 is even (a) I only (b) II only (c) I and II only (d) I and III only
To solve the problem, we need to analyze the implications of the statement "if n3 is odd" and determine the truth of the given statements.
1. Understanding the Condition:
- We start with the condition that n3 is odd.
- In number theory, a number is odd if it cannot be divided evenly by 2.
2. Analyzing n:
- If n3 is odd, we can infer that n must also be odd. This is because the cube of an even number (which is divisible by 2) would also be even. Therefore, if n3 is odd, n cannot be even.
- Thus, Statement I: "n is odd" is true.
3. Analyzing n2:
- Now, since we have established that n is odd, we can analyze n2.
- The square of an odd number is also odd. For example, if n=3 (which is odd), then n2=32=9 (which is also odd). Similarly, if n=5, then n2=52=25.
- Therefore, Statement II: "n^2 is odd" is also true.
4. Analyzing n2 Again:
- Now we check Statement III: "n^2 is even".
- Since we have established that n2 is odd (from the previous step), it cannot be even. Thus, Statement III is false.
Conclusion:
- The true statements are:
- I: n is odd (True)
- II: n^2 is odd (True)
- III: n^2 is even (False)
Thus, the correct answer is (c) I and II only.
- We start with the condition that n3 is odd.
- In number theory, a number is odd if it cannot be divided evenly by 2.
- If n3 is odd, we can infer that n must also be odd. This is because the cube of an even number (which is divisible by 2) would also be even. Therefore, if n3 is odd, n cannot be even.
- Thus, Statement I: "n is odd" is true.
- Now, since we have established that n is odd, we can analyze n2.
- The square of an odd number is also odd. For example, if n=3 (which is odd), then n2=32=9 (which is also odd). Similarly, if n=5, then n2=52=25.
- Therefore, Statement II: "n^2 is odd" is also true.
- Now we check Statement III: "n^2 is even".
- Since we have established that n2 is odd (from the previous step), it cannot be even. Thus, Statement III is false.
- The true statements are:
- I: n is odd (True)
- II: n^2 is odd (True)
- III: n^2 is even (False)
Topper's Solved these Questions
Similar Questions
If n=1+x , where x is the product of four consecutive positive integers, then which of the following is/are true? n is odd II. n is prime III. n is a perfect square. (a) I only (b) I and II only (c) I and III only (d) None of these
View SolutionIf x and y are negative , then which of the following statements is / are always true? x + y is positive. II xy is positive. III. x y is positive. I only (b) II only (c) III only (d) I and III only
View Solution
Knowledge Check
Consider the following statements. For any integer n,
I. n2+3 is never divisible by 17.
II. n2+4 is never divisible by 17.
ThenAboth I and II are trueBboth I and II are falseCI is false and II is trueDI is true and II is false
If x−y=8 , then which of the following must be true? Both x and y are positive. II. If x is negative, y must be positive III. If x is negative, y must be negative. (a) I only (b) II only (c) I and II (d) III only
View SolutionGiven n=1+xandx is product of four consecutive integers. Then which of the following is true? I n is an odd integer II. n is prime. III. n is a perfect square. Only I is correct (b) Only III is correct (c) Both I and II are correct (d) Both I and III are correct
View SolutionJ, L, M, N, O and P are members of a spy network for security reasons, only certain spies are able to contact other spies. The only contacts allowed are:
J can contact both L and N.
O can be contacted by L, M and P.
N can contact M.
O can contact both L and N.
P can be contacted by M.
A spy can receive a message from any spy who can contact him and , in relay the message to any spy he is able to contact.
N can get a message from which of the following spies by using exactly one intermediate contact ?
I. O II.L III.P1) I only 2) III only 3) I and III only 4) II and III only 4) I, II and III
View SolutionIn Figure, which of the following statements must be true? (i) a+b=d+c (ii) a+c+e=1800 (iii) b+f=c+e (a) (i) only (b) (ii) only (c) (iii) only (d) (ii) and (iii) only
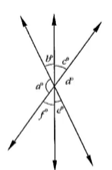
View SolutionShow that the following statement is true: The integer n is even if and only if n2 is even
View SolutionThe sum of three consecutive odd numbers is always divisible by I. 2 II. 3 III. 5 IV. 6 Only I (b) Only II (c) Only I and II (d) Only I and III
View SolutionWhich of the following numbers are completely divisible by 7? I. 195195 II. 181181 III. 120120 IV. 891891 (a) Only I and II (b) Only II and III (c) Only I and IV (d) Only II and IV (e) All are divisible
View Solution
