A car company sold 150 cars in a special 6-day sale. Each day, the company sold 6 more than the previous day. How many cars were sold on the 6th day? (a) 35 (b) 40 (c) 50 (d) 60 (e) 70
To solve the problem step by step, we can follow these instructions:
Step 1: Define the number of cars sold on the first day
Let the number of cars sold on the first day be x.
Step 2: Establish the pattern of sales
According to the problem, each subsequent day, the company sells 6 more cars than the previous day. Therefore, the number of cars sold on each day can be expressed as:
- 1st day: x
- 2nd day: x+6
- 3rd day: x+12
- 4th day: x+18
- 5th day: x+24
- 6th day: x+30
Step 3: Write the equation for total sales
The total number of cars sold over the 6 days is given as 150. We can write the equation:
x+(x+6)+(x+12)+(x+18)+(x+24)+(x+30)=150
Step 4: Simplify the equation
Combining like terms, we have:
6x+(6+12+18+24+30)=150
Calculating the sum of the constants:
6+12+18+24+30=90
Thus, the equation simplifies to:
6x+90=150
Step 5: Solve for x
Subtract 90 from both sides:
6x=150−90
6x=60
Now, divide both sides by 6:
x=10
Step 6: Find the number of cars sold on the 6th day
Now that we have x, we can find the number of cars sold on the 6th day:
Cars sold on the 6th day=x+30=10+30=40
Final Answer
The number of cars sold on the 6th day is 40.
Let the number of cars sold on the first day be x.
According to the problem, each subsequent day, the company sells 6 more cars than the previous day. Therefore, the number of cars sold on each day can be expressed as:
- 1st day: x
- 2nd day: x+6
- 3rd day: x+12
- 4th day: x+18
- 5th day: x+24
- 6th day: x+30
The total number of cars sold over the 6 days is given as 150. We can write the equation:
x+(x+6)+(x+12)+(x+18)+(x+24)+(x+30)=150
Combining like terms, we have:
6x+(6+12+18+24+30)=150
Calculating the sum of the constants:
6+12+18+24+30=90
Thus, the equation simplifies to:
6x+90=150
Subtract 90 from both sides:
6x=150−90
6x=60
Now, divide both sides by 6:
x=10
Now that we have x, we can find the number of cars sold on the 6th day:
Cars sold on the 6th day=x+30=10+30=40
The number of cars sold on the 6th day is 40.
Similar Questions
A car company sold 150 cars in a special 6-day sale. Each day, the company sold 6 more than the previous day. How many cars were sold on the 6th day? (a) 35 (b) 40 (c) 50 (d) 60 (e) 70
View SolutionA can do a work in 12 days. B works60% more fast than A then in how many days B alone could finish this work ?
View Solution
Knowledge Check
A man ate 100 grapes in 5 days. Each day, he ate 6 more grapes than those he ate on the earlier day. How many grapes did he eat on the first day?
A28B26C24D22A man ate 100 grapes in 5 days. Each day, he ate 6 more grapes than those he ate on the earlier day. How many grapes did he eat on the first day ?
A8B12C54D76If the number of cars sold of model D is 40500, then how many more cars of model E are sold than that of A?
A8100B16200C24300D13500
A can finish a work in 14 days at 6 hrs a day. B can finish it in 8 days at 2 hrs a day. Find in how many days they can finish it working together 4 hrs a day.
View SolutionA shoe company sold 50 pairs of shoes on a day costing 189.50 each for 10,000. Then the profit obtained in is
View SolutionStudy the graph carefully and answer the following questions.
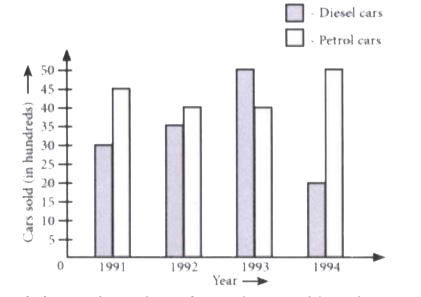
How many more Diesel cars were sold in 1991 than in 1994?
View SolutionA and B complete a work in 6 days. A alone can complete the work in 10 days. In how many days can B alone complete the work ?
View SolutionThe given pie chart shows the quantity wise sales distribution of five products (A, B, C, D and E) of a company in 2016.
दिया गया पाई चार्ट 2016 में एक कंपनी के पाँच उत्पादों ( A, B, C, D और E ) की मात्रा वार बिक्री का वितरण दर्शाता है |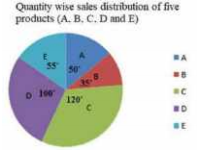 If 320 units of product A were sold by the company, then how many units of products B and E together were sold by the company?
If 320 units of product A were sold by the company, then how many units of products B and E together were sold by the company?
यदि कंपनी के द्वारा वस्तु A की 320 इकाइयाँ बेची गयीं , तो कंपनी के द्वारा बेची गयी वस्तु B और E की कुल इकाइयों की संख्या ज्ञात करें |
View Solution
