A student obtained the following marks in percentages in his semester examination English 50, Maths 65, Statistics 70, Economics 58 and Accountancy 63. The weights of these subjects are 2, 2, 1, 1 and 1 respectively. What is the weighted arithmetic mean? (a) 60 (b) 61 (c) 62 (d) 63
To find the weighted arithmetic mean of the student's marks, we will follow these steps:
Step 1: List the Marks and Weights
We have the following marks and their corresponding weights:
- English: 50% (Weight: 2)
- Maths: 65% (Weight: 2)
- Statistics: 70% (Weight: 1)
- Economics: 58% (Weight: 1)
- Accountancy: 63% (Weight: 1)
Step 2: Calculate the Weighted Marks
We will multiply each mark by its corresponding weight:
- English: 50×2=100
- Maths: 65×2=130
- Statistics: 70×1=70
- Economics: 58×1=58
- Accountancy: 63×1=63
Step 3: Sum the Weighted Marks
Now, we will sum all the weighted marks:
100+130+70+58+63=421
Step 4: Calculate the Total Weight
Next, we will sum the weights:
2+2+1+1+1=7
Step 5: Calculate the Weighted Arithmetic Mean
Finally, we will divide the total weighted marks by the total weight:
Weighted Arithmetic Mean=4217≈60.14
Since we are looking for the closest whole number, we round it to 60.
Conclusion
The weighted arithmetic mean of the student's marks is approximately 60.
We have the following marks and their corresponding weights:
- English: 50% (Weight: 2)
- Maths: 65% (Weight: 2)
- Statistics: 70% (Weight: 1)
- Economics: 58% (Weight: 1)
- Accountancy: 63% (Weight: 1)
We will multiply each mark by its corresponding weight:
- English: 50×2=100
- Maths: 65×2=130
- Statistics: 70×1=70
- Economics: 58×1=58
- Accountancy: 63×1=63
Now, we will sum all the weighted marks:
100+130+70+58+63=421
Next, we will sum the weights:
2+2+1+1+1=7
Finally, we will divide the total weighted marks by the total weight:
Weighted Arithmetic Mean=4217≈60.14
The weighted arithmetic mean of the student's marks is approximately 60.
Topper's Solved these Questions
Similar Questions
A student obtains the following percentage in an examination.
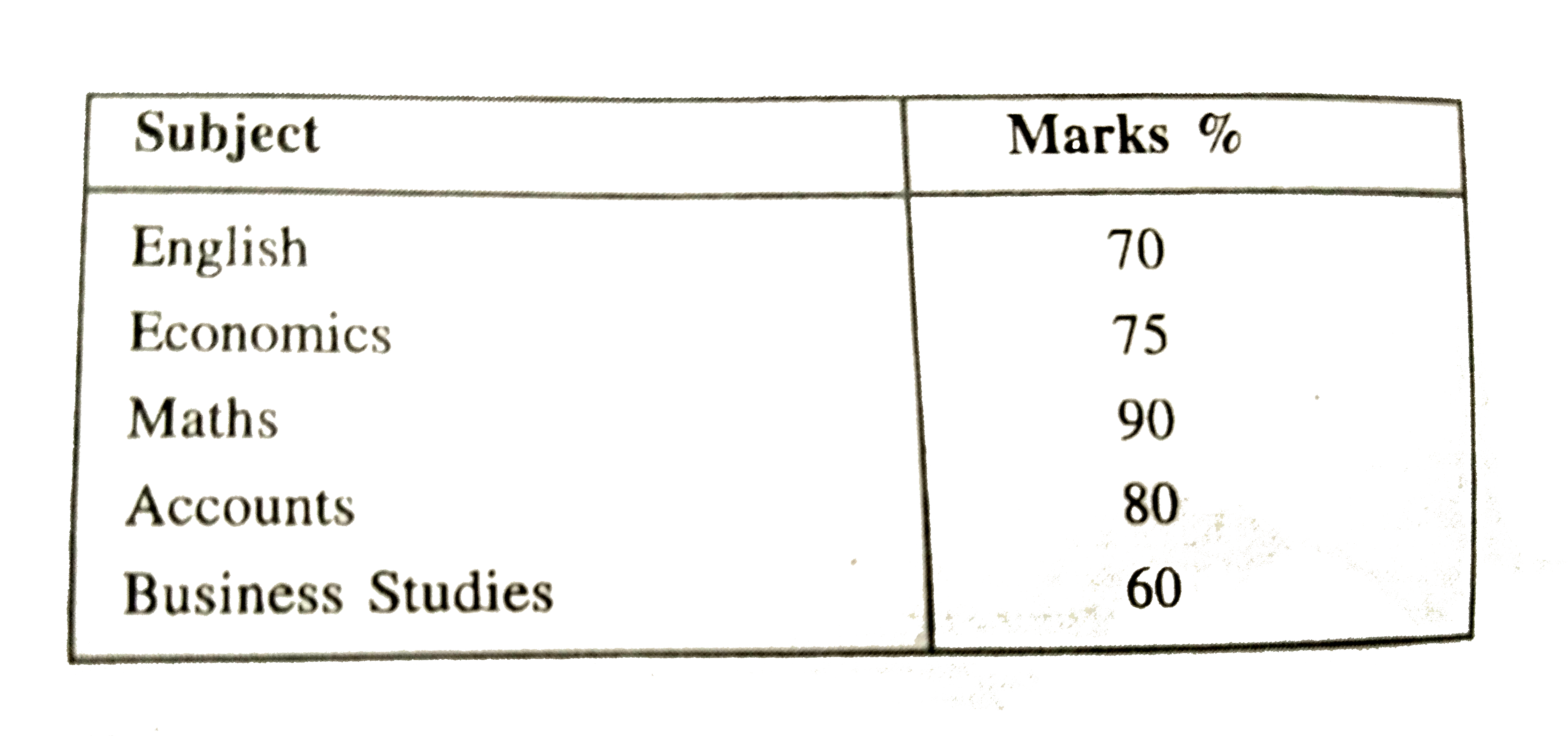
(i) Find out simple mean marks , if all subjectes are given equal weight.
(ii) Find out weighted mean marks, if the respective weights are 1,2,1,2,3
View SolutionA student obtained 60 marks in English, 75 in Hindi, 63 in Mathematics, 59 in Economics and 55 in Statistics. Calculate weighted mean of the marks if weights are respectively 2, 1, 5, 5 and 3.
View Solution
Knowledge Check
A student obtained the following marks per centage in an examination English - 50, Accounts - 75, Economics - 60, B Std.-80, Hindi - 55. If weights are 2, 3, 3, 2, 1, respectively allotted to the subjects, his weighted mean is
A50+75+60+80+552+3+3+2+1B(50×2)+(75×3)+(60×3)+(80×2)+(55×1)5C50×2+75×3+60×3+80×+55×12+3+3+2+1DnoneA candidate obtained the following percentage of marks in an examination English 60, Maths 90, Physics 75, Chemistry 66. If weighs 2, 4, 3, 3 are allotted to these subjects respectively, then the weight mean is given by
A60+90+75+662+4+3+3B60×2+90×4+75×3+66×32+4+3+3C60×2+90×4+75×3+66×34D60+90+75+664A candidate obtains the marks in subjects, English 40, Hindi 30, Mathematics 60, Physics 70 and Chemistry 40. In the weights of 1, 2, 2, 3, 3 respectively are allotted to the subjects, then in the candidates weighted mean is
A59B615C10D50
A student obtained 60 marks in English, 75 in Hindi, 63 in Mathematics, 59 in Economics and 55 in Statistics. Calculate weighted mean of the marks if weights are respectively 2, 1, 5, 5 and 3.
View SolutionThe average marks in Science subject of a class of 20 students is 68. If the marks of two students were misread as 48 and 65 instead of the actual marks 72 and 61 respectively, what would be the correct average? (a) 66 (b) 68.5 (c) 69 (d) 69.5 (e) 70
View SolutionIn a class with a certain number of students, if one student weighing 50 kg is added then the average weight of the class increases by 1 kg. If one more student weighing 50 kg is added, then the average weight of the class increases by 1.5 kg over the original average. What is the original average weight (in kg) of the class? (a) 2 (b) 4 (c) 46 (d) 47
View SolutionA candidate obtains the marks in subjects English 60 Hindi 75 , Mathematics 63 , Physics 59 and Chemistry 55 . In the weights of 1,2,1,3,3 respectively are alloted to the subjects then the candidates weighted mean is
View SolutionIn an examination, a candidate scores the following percentage of marks. English-44, Hindi-58, Maths—74, Physics-61, Chemistry—62. If weights 2, 4, 4, 5, 3 respectively, are allotted to these subjects, then the candidate's weighted mean percentage is
View Solution
