A particle slides on frictionless x - y plane. It is acted on by a conservative force described by the potential - energy function U(x,y)=12k(x2+y2). Derive an expression for the force acting on the particle.
To derive the expression for the force acting on the particle given the potential energy function U(x,y)=12k(x2+y2), we will follow these steps:
Step 1: Understand the relationship between force and potential energy
The force F acting on a particle in a conservative field is related to the potential energy U by the equation:
F=−∇U
where ∇U is the gradient of the potential energy function.
Step 2: Calculate the gradient of the potential energy function
The potential energy function given is:
U(x,y)=12k(x2+y2)
To find the force, we need to compute the gradient ∇U. The gradient in two dimensions is given by:
∇U=(∂U∂x,∂U∂y)
Step 3: Compute the partial derivatives
1. Partial derivative with respect to x:
∂U∂x=∂∂x(12k(x2+y2))=12k⋅2x=kx
2. Partial derivative with respect to y:
∂U∂y=∂∂y(12k(x2+y2))=12k⋅2y=ky
Step 4: Write the gradient vector
Now we can write the gradient vector:
∇U=(kx,ky)
Step 5: Calculate the force vector
Using the relationship F=−∇U:
F=−(kx,ky)=(−kx,−ky)
Step 6: Express the force in vector form
In vector notation, we can express the force as:
F=−kx^i−ky^j
Final Expression
Thus, the expression for the force acting on the particle is:
F=−k(x^i+y^j)
The force F acting on a particle in a conservative field is related to the potential energy U by the equation:
F=−∇U
where ∇U is the gradient of the potential energy function.
The potential energy function given is:
U(x,y)=12k(x2+y2)
To find the force, we need to compute the gradient ∇U. The gradient in two dimensions is given by:
∇U=(∂U∂x,∂U∂y)
1. Partial derivative with respect to x:
∂U∂x=∂∂x(12k(x2+y2))=12k⋅2x=kx
∂U∂y=∂∂y(12k(x2+y2))=12k⋅2y=ky
Now we can write the gradient vector:
∇U=(kx,ky)
Using the relationship F=−∇U:
F=−(kx,ky)=(−kx,−ky)
In vector notation, we can express the force as:
F=−kx^i−ky^j
Thus, the expression for the force acting on the particle is:
F=−k(x^i+y^j)
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle is moving on frictionless XY-plane. It is acted on by a conservative force described by the potential-energy function.
U(x,y,z)=12k(x2+y2+z2)
where , k=constant
Derive an expression for the force an the particle.
View SolutionIf the potential energy function of a particle is given by U=−(x2+y2+z2)J, whre x,y and z are in meters. Find the force acting on the particle at point A(1m,3m,5m).
View Solution
Knowledge Check
The potential energy of a force filed →F is given by U(x,y)=sin(x+y). The force acting on the particle of mass m at (0,π4) is
A1B√2C1√2D0As a particle moves along the x−axis, it is acted upon by a conservative force. The potential energy is shown below as a function of the coordinate x of the particle. Rank the labelled regions accoeording to the magnitude of force, least to greatest.
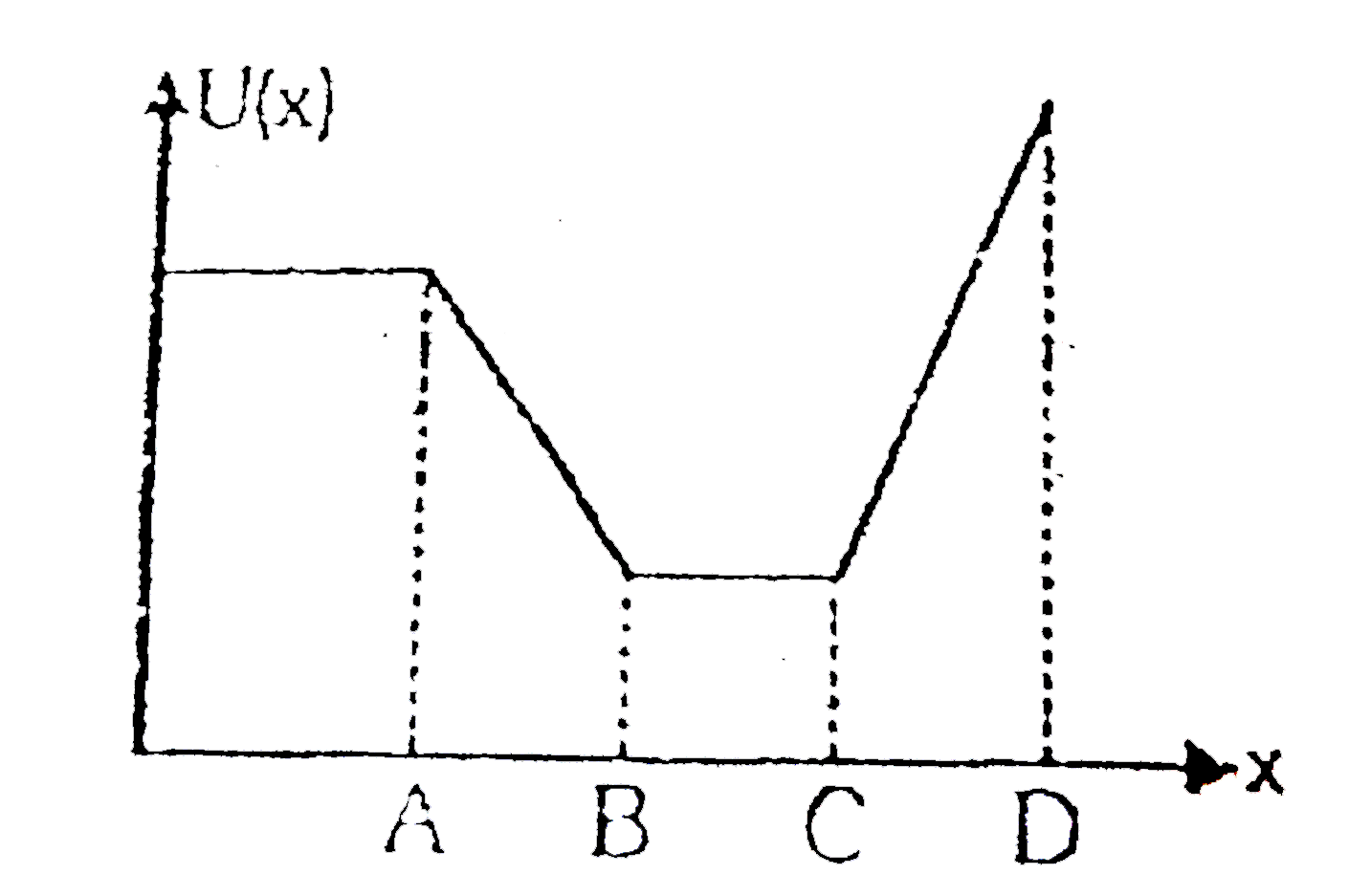 AAB, BC, CDBAB, CD, BCCBC, CD, ABDBC, AB, CD
AAB, BC, CDBAB, CD, BCCBC, CD, ABDBC, AB, CDThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
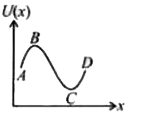 ACBBCB and CDA and D
ACBBCB and CDA and D
A particle is moving in a potential region defined by U=K(x2+y2+z2). Calculate the force acting on the particle.
View SolutionThe motion of a particle of mass m is described by y=ut+12gt2 . Find the force acting on the particale .
View SolutionThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at

View SolutionThe potential energy of a body is given by U=A−Bx2 (where x is the displacement). The magnitude of force acting on the partical is
View SolutionFigure given below shows the variation of potential energy function U(x), corresponding to a particle lying in a one dimensional force field. The force acting on the particle at x = 2 m is:
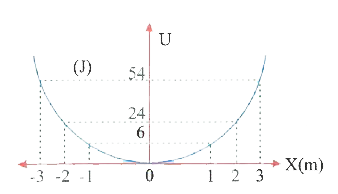
View Solution