The blades of a windmill sweep out a circle of area A. If the wind flows at a velocity v perpendicular to the circle, then the mass of the air of density ρ passing through it in time t is
ρAv32
ρAv22
ρAv2
2ρAv2
The correct Answer is:A
Step by step video, text & image solution for The blades of a windmill sweep out a circle of area A. If the wind flows at a velocity v perpendicular to the circle, then the mass of the air of density rho passing through it in time t is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
39 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - C)
80 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE
40 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
The blades of a windmill sweep out a circle of area A. (a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through in time t? (b) What is the kinetic energy of the air? (c) Assume that the windmill converts 25% of the wind's energy into electrical energy, and that A=30m2, v=36kmh−1 and the density of air is 1.2kgm−3, what is the electrical power produced?
View SolutionThe blades of a windmill sweep out a circle of area A. (a) If the wind flows at a velocity υ perpendicular to the circle, what is the mass of air passing through it in time t? (b) What is K.E. of the air ? (c) Assume that the wind mill converts 25% of the wind's energy into electrical energy , and that A=30m2,υ=36km/h and the density of air is 1.2kg/m3. What is electrical power produced ?
View Solution
Knowledge Check
The blades of a wind mill sweep out a circle of area A. If wind flows with velocity v perpendicular to blades of wind mill and its density is p, then the mechanical power received by wind mill is
ApAv32BpAv22CpAv2D2pAv2A copper rod is bent inot a semi-circle of radius a and at ends straight parts are bent along diameter of the semi-circle and are passed through fixed, smooth and conducting ring O and O' as shown in figure. A capacitor having capacitance C is connected to the rings. The system is located in a uniform magnetic field of induction B such that axis of rotation OO' is perpendicular to the field direction. At initial moment of time (t=0), plane of semi-circle was normal to the field direction and the semi-circle is set in rotation with constant angular velocity ω. Neglect the resistance and inductance of the circuit. The current flowing through the circuit as function of time is
 A14πω2a2CBcosωtB12πω2a2CBcosωtC14πω2a2CBsinωtD12πω2a2CBsinωt
A14πω2a2CBcosωtB12πω2a2CBcosωtC14πω2a2CBsinωtD12πω2a2CBsinωtThe air of density ρ and moving with a velocity v strikes perpendicular the inclined surface of area A and of a wedge kept on a horizontal surface. The mass of the wedge is m. Assuming the collisions to be perfectly inelastic, the minimum value of the coefficient of friction between the wedge and the ground so that the wedge does not move is (Assume mass of particles of air is negligible)
 AρAv2sinθmg+ρAv2cosθBtanθCρAv2mgtanθDρAv2mg+ρAv2cosθ
AρAv2sinθmg+ρAv2cosθBtanθCρAv2mgtanθDρAv2mg+ρAv2cosθ
The power P delivered by a windmill whose blades sweep in a circle of diameter D by a wind of speed v is proportional to the square of the diameter and the cube of the wind speed. Show that this dependence on diameter and wind speed exist when 100% energy transfer takes place. Also show that
P=π8ρD2v3
Where is ρ the density of air.
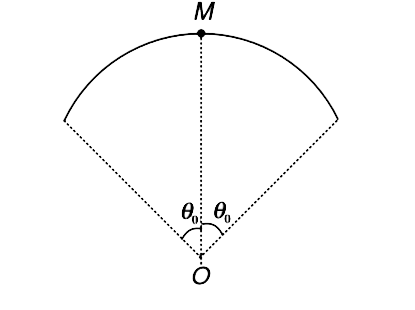
View SolutionA wire of linear mass density λ(kg/m) is bent into an arc of a circle of radius R subtending an angle 2θ0 at the centre. Calculate the moment o inertia of this circular arc about an axis passing through its midpoint (M) and perpendicular to its plane.
View SolutionThe surface density (mass/area) of a circular disc of radius a depends on the distance from the centre as ρ(r)=A+Br. Find its moment of inertia about the line perpendicular to the plane of the disc through its centre.
View SolutionThe flow speeds of air on the lower and upper surfaces of the wing ofan aeroplane are v and √2v respectively. A is the area of the wing and ρ is the density of th e surrounding air. What is the force of the dynamic lift on the wing ?
View SolutionA particle rotates in U.C.M with tengential velocity 'v' along a ghorizontal circle of diameter 'D' . Total angular displacement of the particle in time 't' is
View Solution
