The work done by an applied variable force F=x+x3 from x = 0 m to x = 2m, where x is displacement, is
6 J
8 J
10 J
12 J
The correct Answer is:A
To find the work done by the variable force F=x+x3 from x=0m to x=2m, we will use the concept of integration. The work done W by a force is given by the integral of the force over the displacement:
W=∫x2x1Fdx
1. Identify the Force Function:
The given force function is F=x+x3.
2. Set Up the Integral:
We need to integrate the force from x=0 to x=2:
W=∫20(x+x3)dx
3. Split the Integral:
We can split the integral into two parts:
W=∫20xdx+∫20x3dx
4. Calculate Each Integral:
- For the first integral:
∫xdx=x22
Evaluating from 0 to 2:
(x22)20=222−022=42−0=2
- For the second integral:
∫x3dx=x44
Evaluating from 0 to 2:
(x44)20=244−044=164−0=4
5. Combine the Results:
Now, we add the results of both integrals:
W=2+4=6Joules
Final Answer:
The work done by the applied variable force from x=0m to x=2m is 6J.
---
The given force function is F=x+x3.
We need to integrate the force from x=0 to x=2:
W=∫20(x+x3)dx
We can split the integral into two parts:
W=∫20xdx+∫20x3dx
- For the first integral:
∫xdx=x22
Evaluating from 0 to 2:
(x22)20=222−022=42−0=2
∫x3dx=x44
Evaluating from 0 to 2:
(x44)20=244−044=164−0=4
Now, we add the results of both integrals:
W=2+4=6Joules
The work done by the applied variable force from x=0m to x=2m is 6J.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
15 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
39 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle is subjected to a force Fx that varies withes position as shown in figure. Find the work done by the force on the body as it moves
(a) from x=10.0m to x=5.0m,
(b) from x=5.0m to x=10.0m,
(c ) from x=10.0m to x=15.0m,
(d) what is the total work done by the force over the distance x=0 to x=15.0?
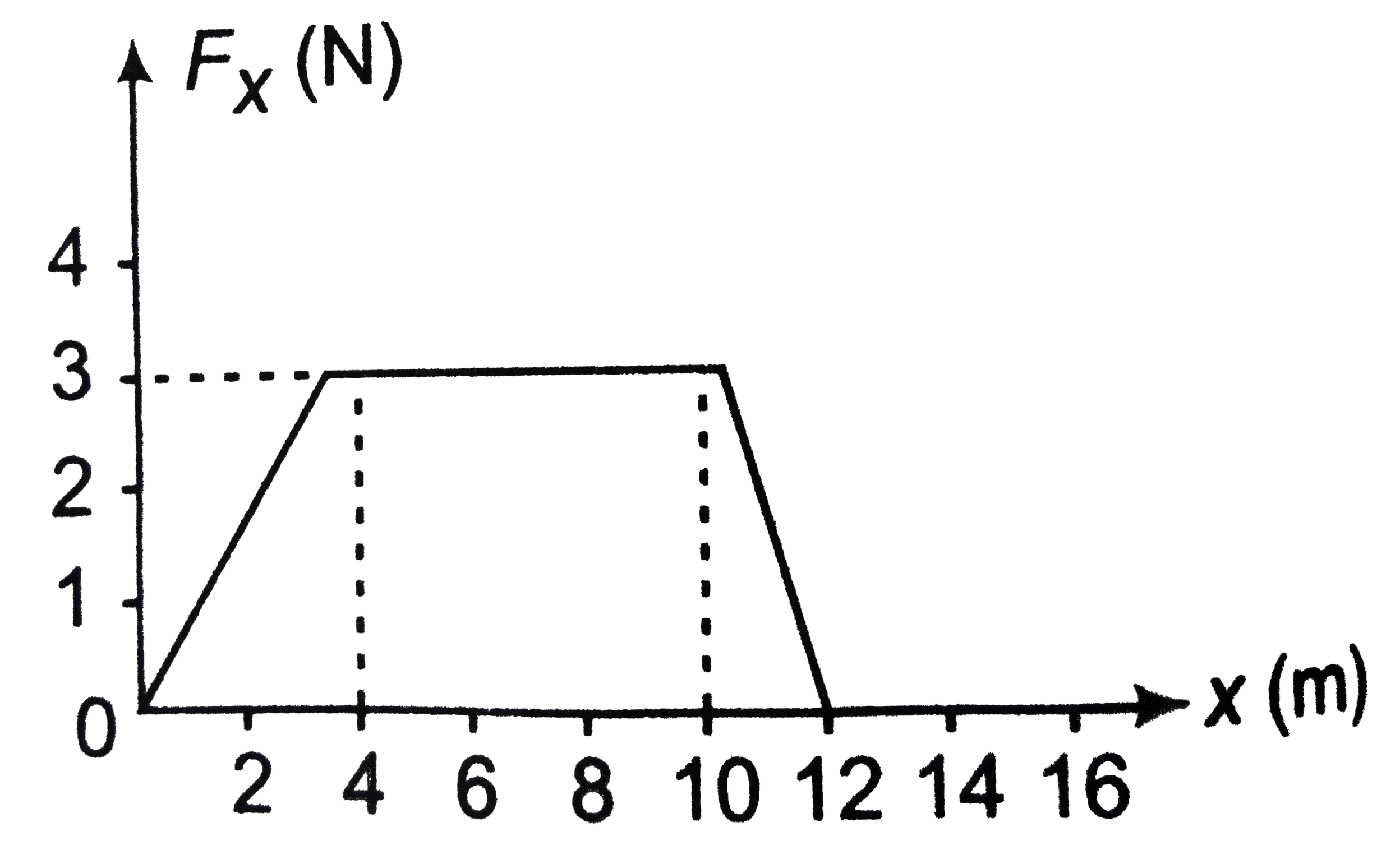 .
.
View SolutionFigure gives the acceleration of a 2 . 0 kg body as it moves from rest along x - axis while a variable force acts on it from x = 0 m to x = 9 m . Find the work done by the force of the body when it reaches
x = 4 m and
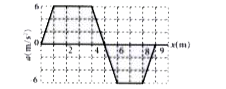
View Solution
Knowledge Check
A force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
A−k2aB−kaC−2kaD−akThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
A−240JB360JC420JDwill depend upon the pathA force Fy=(3x+2) N is acting on a body. The work done by this force if it tends to displace the body from x = 0 m to x = 4 m will be
A32 JB16 JC0 JD(12x+8) J
Figure gives the acceleration of a 2 . 0 kg body as it moves from rest along x - axis while a variable force acts on it from x = 0 m to x = 9 m . Find the work done by the force of the body when it reaches
x = 7 m
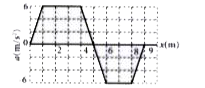
View SolutionA particle moves under the effect of a force F=kx2 from x=0 to x=4, the work done by force is ?
View SolutionA force (F) acting on a particle varoes work done by a particle varies with the with the position x as shown in figure
 .
.
Find the work done by by force in displacing the particle from .
(a) x=−2m to x=0
(b) x=0 to x=2m..
View SolutionA force F=(10+0.5x) acts on a particle in the x-direction. What would be the work done by this force during a displacement from x=0 to x=2m (F is in newton and x in metre)
View SolutionA force F = (2+ x)N acts on a particle in the x-direction. The work done by this force during a displacement from x = 1.0 m to x = 2.0 m is
View Solution
