Let be the angle between vectors . Which of the following figures correctly represent the angle ?
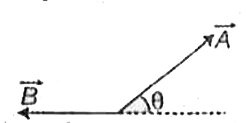

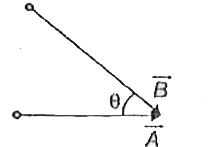
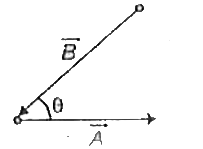
The correct Answer is:C
To determine the correct representation of the angle θ between the vectors →A and →B, we can follow these steps:
1. Understand the Definition of Angle Between Vectors:
The angle θ between two vectors is defined as the angle formed when the vectors are placed tail-to-tail or head-to-head.
2. Identify the Vectors:
Let →A and →B be two vectors. Each vector has a tail (starting point) and a head (ending point).
3. Visualize the Vectors:
Draw the vectors →A and →B such that their tails are at the same point. This means both vectors are originating from the same point.
4. Determine the Angle:
The angle θ is the angle formed between the two vectors when they are drawn from the same point. This angle is considered to be the smaller angle (acute angle) between the two vectors.
5. Analyze the Options:
- Look for the figure that shows the angle θ formed between the tails of →A and →B.
- Ensure that the angle is acute (less than 90 degrees).
6. Select the Correct Figure:
Based on the analysis, choose the figure that correctly represents the angle θ as the angle between the two vectors →A and →B when they are positioned tail-to-tail or head-to-head.
Conclusion:
The correct representation of the angle θ between vectors →A and →B is the figure that shows the acute angle formed at the point where the tails of both vectors meet.
---
The angle θ between two vectors is defined as the angle formed when the vectors are placed tail-to-tail or head-to-head.
Let →A and →B be two vectors. Each vector has a tail (starting point) and a head (ending point).
Draw the vectors →A and →B such that their tails are at the same point. This means both vectors are originating from the same point.
The angle θ is the angle formed between the two vectors when they are drawn from the same point. This angle is considered to be the smaller angle (acute angle) between the two vectors.
- Look for the figure that shows the angle θ formed between the tails of →A and →B.
- Ensure that the angle is acute (less than 90 degrees).
Based on the analysis, choose the figure that correctly represents the angle θ as the angle between the two vectors →A and →B when they are positioned tail-to-tail or head-to-head.
The correct representation of the angle θ between vectors →A and →B is the figure that shows the acute angle formed at the point where the tails of both vectors meet.
Similar Questions
Knowledge Check
If the angle between two vectors →Aand→B is 90∘ then
A→A=2→BB→A−→B=→0C∣∣→A+→B∣∣=∣∣→A−→B∣∣D→A+→B=→0The angle between vectors (→A×→B)and(→B×→A) is :
Aπ radBπ2 radCπ4 radDzeroIf θ is smaller angle between force vector →F and velocity vector →v then Fv cos θ represents
AworkBpowerCkinetic energyDcentripetal force
The angle between the vectors →Aand→B is θ. The value of →A(→A×→B) is -
View SolutionIf θ is the angle between unit vectors →A and →B, then (1−→A.→B)1+→A.→B⎞⎟ ⎟⎠ is equal to
View SolutionIf the angle between the vectors →Aand→B is θ, the value of the product (→B×→A)⋅→A is equal to
View SolutionIf the angle between the vectors →Aand→B is θ, the value of the product (→B×→A)⋅→A is equal to
View SolutionThe angle between the vector →A and →B is θ. The value of the triple product →A.(→B×→A) is
View Solution

