A shell is fired vertically upwards with a velocity v1 from a trolley moving horizontally with velocity v2. A person on the the ground observes the motion of the shell as a parabole, whose horizontal range is
2v21v2g
2v21g
2v22g
2v1v2g
The correct Answer is:D
To solve the problem of finding the horizontal range of a shell fired vertically upwards from a trolley moving horizontally, we can break down the solution into the following steps:
Step 1: Understand the Motion
The shell is fired vertically upwards with a velocity v1 from a trolley that is moving horizontally with a velocity v2. The motion of the shell can be analyzed in two dimensions: vertical and horizontal.
Hint: Remember that the horizontal and vertical motions are independent of each other.
Step 2: Identify the Components of Velocity
- The horizontal component of the shell's velocity (ux) is equal to the velocity of the trolley, which is v2.
- The vertical component of the shell's velocity (uy) is equal to the velocity with which it is fired upwards, which is v1.
Hint: Write down the equations for horizontal and vertical components of motion separately.
Step 3: Determine the Time of Flight
The time of flight (t) for the shell can be determined by analyzing the vertical motion. The time taken for the shell to reach its maximum height and return to the original height can be calculated using the formula:
t=2uyg=2v1g
where g is the acceleration due to gravity.
Hint: Use the kinematic equations for vertical motion to find the time of flight.
Step 4: Calculate the Horizontal Range
The horizontal range (R) can be calculated using the horizontal velocity and the time of flight:
R=ux⋅t=v2⋅t
Substituting the expression for t:
R=v2⋅2v1g
Thus, the horizontal range is:
R=2v1v2g
Hint: Remember that the horizontal range is the product of horizontal velocity and time of flight.
Final Answer
The horizontal range of the shell observed by a person on the ground is:
R=2v1v2g
The shell is fired vertically upwards with a velocity v1 from a trolley that is moving horizontally with a velocity v2. The motion of the shell can be analyzed in two dimensions: vertical and horizontal.
- The horizontal component of the shell's velocity (ux) is equal to the velocity of the trolley, which is v2.
- The vertical component of the shell's velocity (uy) is equal to the velocity with which it is fired upwards, which is v1.
The time of flight (t) for the shell can be determined by analyzing the vertical motion. The time taken for the shell to reach its maximum height and return to the original height can be calculated using the formula:
t=2uyg=2v1g
where g is the acceleration due to gravity.
The horizontal range (R) can be calculated using the horizontal velocity and the time of flight:
R=ux⋅t=v2⋅t
Substituting the expression for t:
R=v2⋅2v1g
Thus, the horizontal range is:
R=2v1v2g
The horizontal range of the shell observed by a person on the ground is:
R=2v1v2g
Similar Questions
A ball A is falling vertically downwards with velocity v1 . It strikes elastically with a wedge moving horizontally with velocity v2 as shown in figure . What must be the ratio v1v2 , so that the ball bounces back in vertically upward direction relative to the wedge
 View Solution
View SolutionA stone projected vertically up with velocity v from the top of a tower reaches the ground with velocity 2 v The height of the tower
View Solution
Knowledge Check
- Question 1 - Select One
A shell is fired vertically upwards with a velocity v1 from the deck of a ship travelling at a speed of v2 . A person on the shore observes the motion of the shell as parabola. Its horizontal range is given by:
A2v2gB2v1v22gC2v1v2gD2v21v22g - Question 2 - Select One
If block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
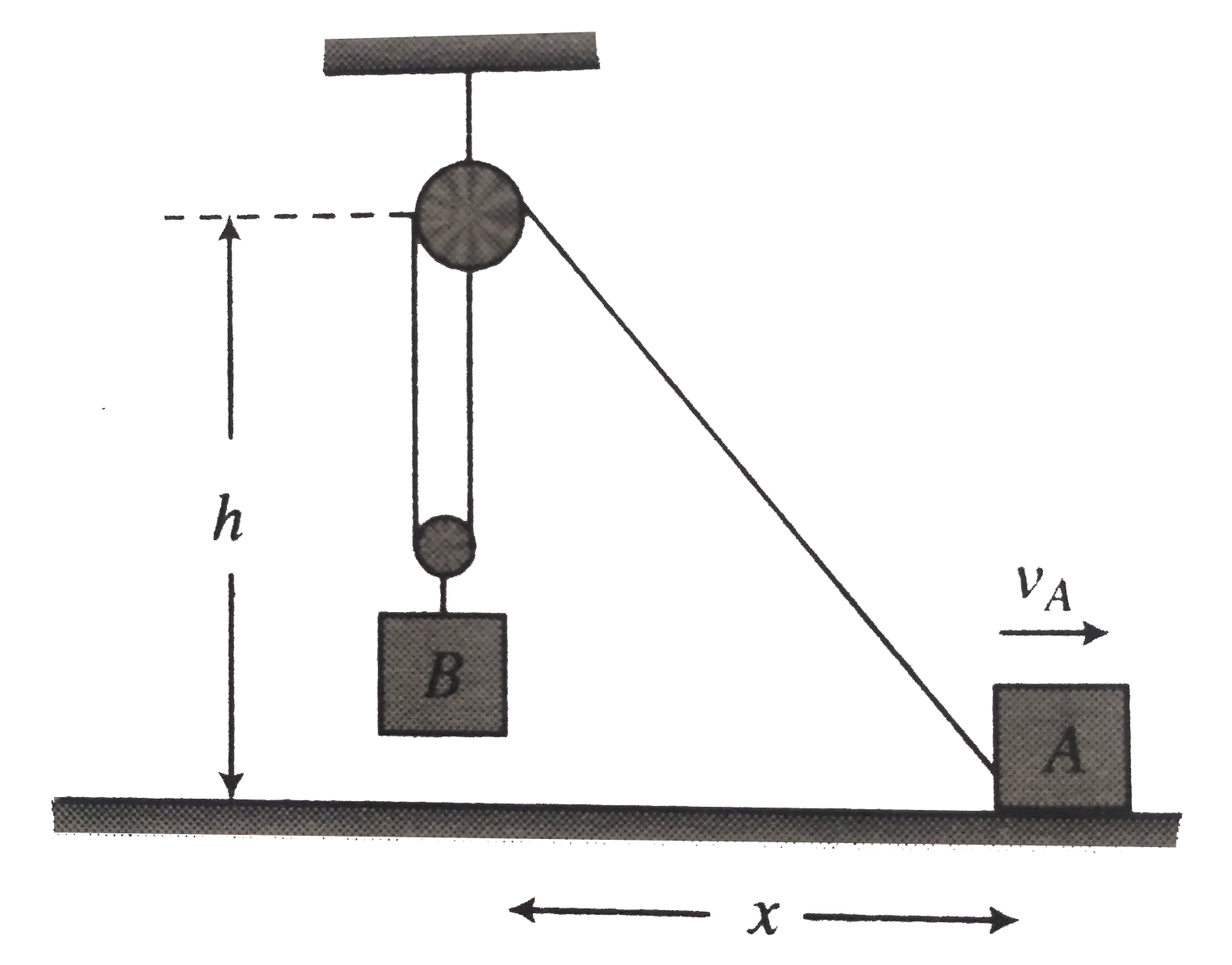 AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2
AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2 - Question 3 - Select One
A particle is thrown vertically upwards with a velocity v. It returns to the ground in time T. which of the following graphs correctly represents the motion ?
A B
B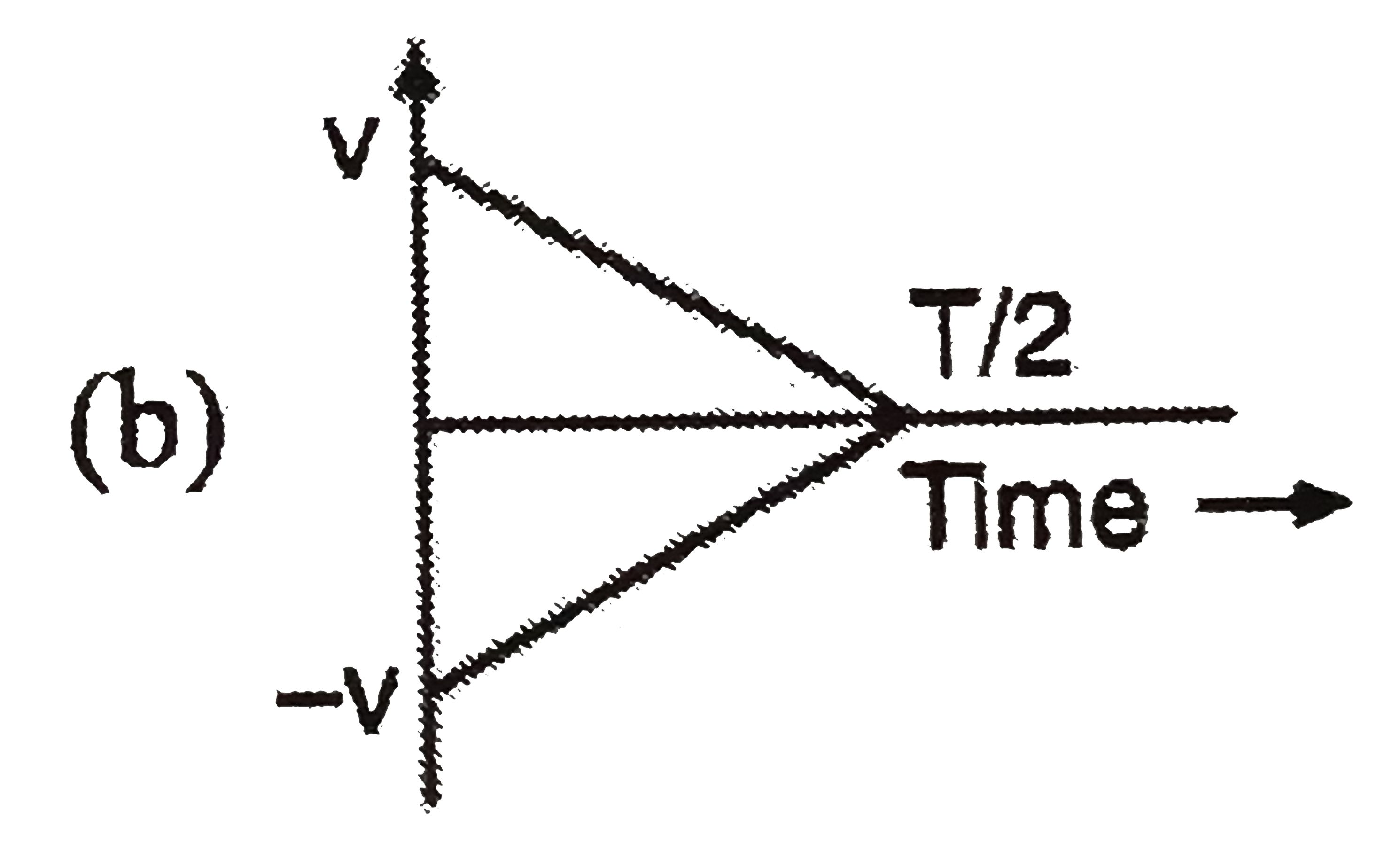 C
C D
D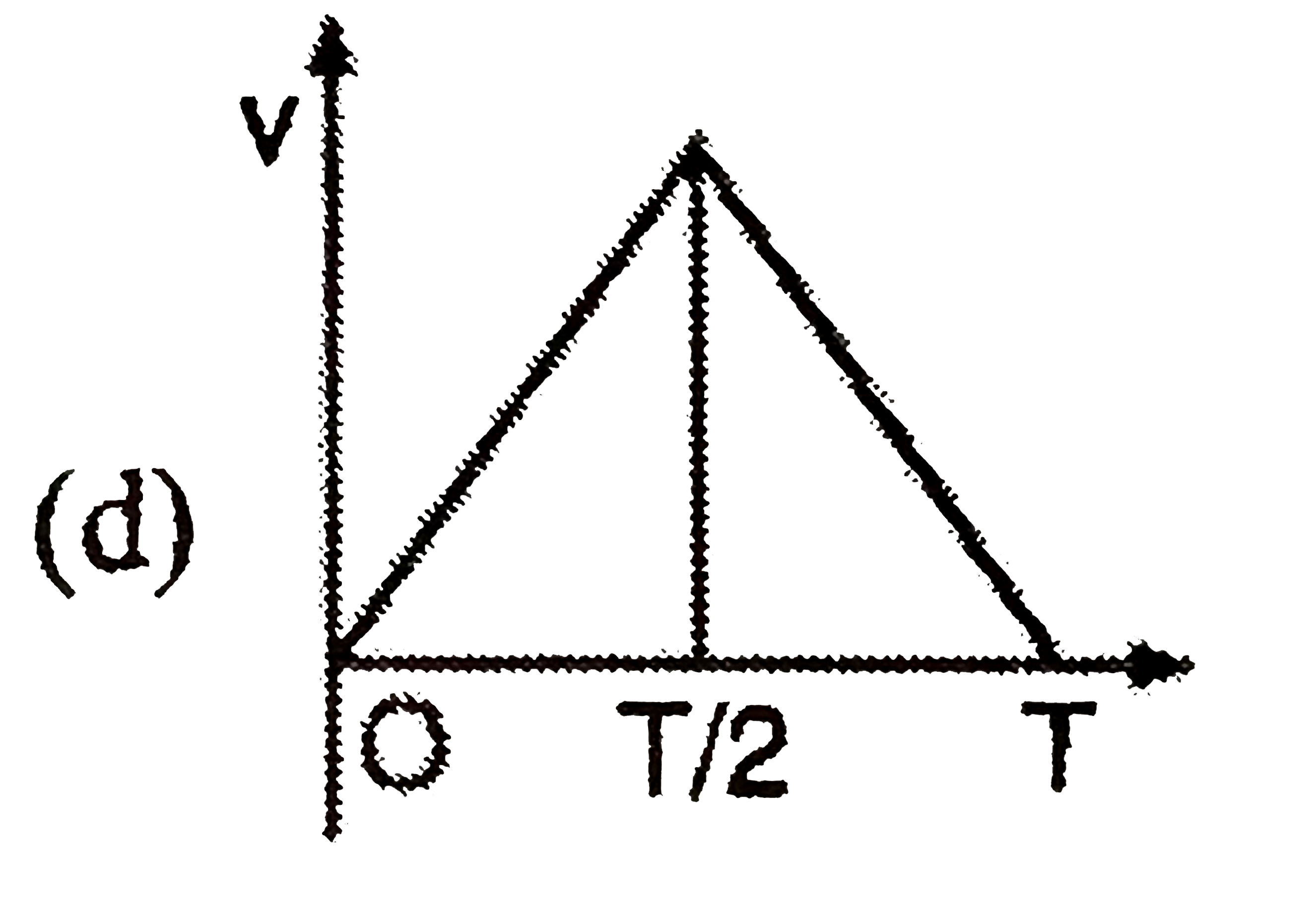
A stone projected vertically up with velocity v from the top of a tower reaches the ground with velocity 2v .The height of the tower is
View SolutionA particle is projected vertically upwards with a velocity v. It returns to the ground in time T. Which of the following graphs correctly represents the motion.
View SolutionA bullet is fired vertically upwards with velocity v form the surface of a spherical planet. If the escape velocity from the planet is vesc=v√N, then the value of N is (ignore energy loss due to atmosphere)
View SolutionA projectile is thrown upward with a velocity v0 at an angle α to the horizontal. The change in velocity of the projectile when it strikes the same horizontal plane is
View SolutionConsider a shell that has a muzzle velocity of 45ms−1 fired from the tail gun of an airplane moving horizontally with a velocity of 215ms−1 . The tail gun can be directed at any angle with the vertical in the plane of motion of the airplane. The shell is fired when the plane is above point A on ground, and the plane is above point B on ground when the shell hits the ground. (Assume for simplicity that the Earth is flat)
View Solution

