Two paper screens A and B are separated by distance 100 m. A bullet penetrates A and B, at points P and Q respectively, where Q is 10 cm below P. If bullet is travelling horizotally at the time of hitting A, the velocity of bullet at A is nearly
100 m/s
200 m/s
600 m/s
700 m/s
The correct Answer is:D
To solve the problem, we need to analyze the motion of the bullet as it travels horizontally and falls vertically due to gravity. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have two screens A and B separated by a distance of 100 m. The bullet travels horizontally and penetrates both screens at points P and Q, where Q is 10 cm below P. We need to find the velocity of the bullet at screen A.
Step 2: Identify the Vertical Motion
The bullet falls vertically due to gravity while traveling horizontally. The vertical distance fallen (from P to Q) is 10 cm, which is equal to 0.1 m.
Step 3: Use the Equation of Motion
We can use the second equation of motion for vertical displacement:
s=ut+12at2
Here,
- s is the vertical displacement (0.1 m),
- u is the initial vertical velocity (0 m/s, since it starts falling from rest),
- a is the acceleration due to gravity (approximately 9.81m/s2),
- t is the time taken to fall.
Substituting the values, we have:
0.1=0+12⋅9.81⋅t2
This simplifies to:
0.1=4.905t2
Step 4: Solve for Time t
Rearranging the equation gives:
t2=0.14.905
Calculating this:
t2≈0.0204⇒t≈√0.0204≈0.142s
Step 5: Calculate Horizontal Velocity
Now, we know the bullet travels horizontally a distance of 100 m in the time t. Using the formula:
Distance=Velocity×Time
We can rearrange it to find the horizontal velocity v:
v=Distancet=1000.142
Calculating this gives:
v≈704.2m/s
Step 6: Final Answer
Thus, the velocity of the bullet at screen A is approximately 700 m/s (rounded to the nearest hundred).
We have two screens A and B separated by a distance of 100 m. The bullet travels horizontally and penetrates both screens at points P and Q, where Q is 10 cm below P. We need to find the velocity of the bullet at screen A.
The bullet falls vertically due to gravity while traveling horizontally. The vertical distance fallen (from P to Q) is 10 cm, which is equal to 0.1 m.
We can use the second equation of motion for vertical displacement:
s=ut+12at2
Here,
- s is the vertical displacement (0.1 m),
- u is the initial vertical velocity (0 m/s, since it starts falling from rest),
- a is the acceleration due to gravity (approximately 9.81m/s2),
- t is the time taken to fall.
0.1=0+12⋅9.81⋅t2
This simplifies to:
0.1=4.905t2
Rearranging the equation gives:
t2=0.14.905
Calculating this:
t2≈0.0204⇒t≈√0.0204≈0.142s
Now, we know the bullet travels horizontally a distance of 100 m in the time t. Using the formula:
Distance=Velocity×Time
We can rearrange it to find the horizontal velocity v:
v=Distancet=1000.142
Calculating this gives:
v≈704.2m/s
Thus, the velocity of the bullet at screen A is approximately 700 m/s (rounded to the nearest hundred).
Similar Questions
Two paper screens A and B are separated by a distance of 100m. A bullet pierces A and B. The hole in B is 10cm below the hole in A. If the bullet is travelling horizontally at the time of hitting the screen A, calculate the velocity of the bullet when it hits the screen A. Neglect resistance of paper and air.
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
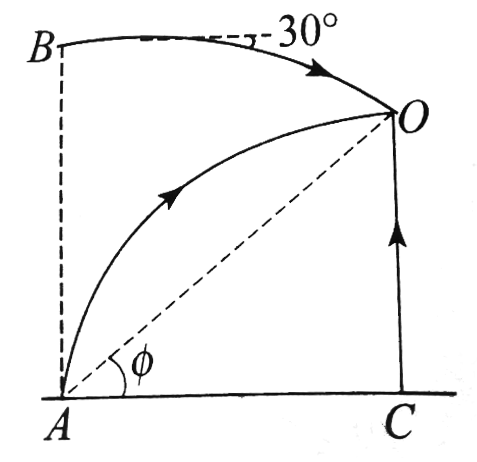
Find the time in which bullets will collide (seconds ):
View Solution
Knowledge Check
Two paper screens A and B are separated by a distance of 200 m. A bullet pierces A and then B. The hole in B is 40 cm below the hole in A. If the bullet is travelling horizontally at the time of hitting A, then the velocity of the bullet at A is
A200ms−1B400ms−1C600ms−1D700ms−1Two paper screens A and B are separated by 150m. A bullet pierces A and B. The hole in B in 15 cm below the hole in A. If the bullet is travelling horizontally at the time of hitting A, then the velocity of the bullet at A is: (g=10ms−2)
A100√3ms−1B200√3ms−1C300√3ms−1D500√3ms−1Two thin wood screens A and B are separated by 200m a bullet travelling horizontally at speed of 600m/s hits the screen A penetrates through it and finally emerges out from B making holes in A and B the resistance of air and wood are negligible the difference of heights of the holes in A and B is.
A5mB4990mC7√90mDzero
Points A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
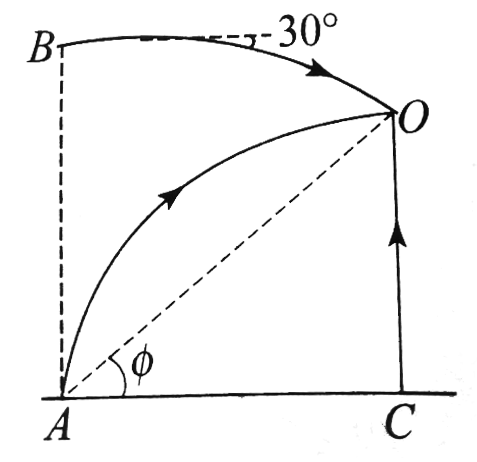
Find the velocity of bullet at A:
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.

Find the elevation angle ∠θ=∠OAC:
View SolutionIn the given figure points A and C are on the horizontal ground & A and B are in same vertical plane. Simultaneously bullets are fired from A, B and C and they collide at D. The bullet at B is fired horizontally with speed of 725km/hr and the bullet at C is projected vertically upward at velocity of 545km/hr. Find velocity of the bullet projected from A in m/s.

View SolutionTwo points P and Q are maintained at the potentials of 10 V and - 4 V respectively. The work done in moving 100 electrons from P to Q is
View SolutionTwo points P and Q are maintained at the potentials of 10V and -4V, respectively. The work done in moving 100 electrons from P to Q is:
View Solution
