A particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
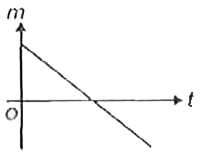

The correct Answer is:A
To solve the problem of how the slope (m) of the trajectory of a particle projected at an angle θ with the horizontal varies with time (t), we can follow these steps:
Step 1: Understand the Motion Components
The particle is projected with an initial speed u at an angle θ. We can break this motion into horizontal and vertical components:
- Horizontal component of velocity: ux=ucosθ
- Vertical component of velocity: uy=usinθ
Step 2: Write the Equations of Motion
For horizontal motion (x-direction):
- There is no acceleration, so the position as a function of time is given by:
x=uxt=ucosθ⋅t
For vertical motion (y-direction):
- The vertical position as a function of time is given by:
y=uyt−12gt2=usinθ⋅t−12gt2
Step 3: Eliminate Time to Find the Trajectory Equation
We can express time t in terms of x from the horizontal motion equation:
t=xucosθ
Substituting this expression for t into the vertical motion equation:
y=usinθ(xucosθ)−12g(xucosθ)2
This simplifies to:
y=xtanθ−g2u2cos2θx2
This is the equation of the trajectory.
Step 4: Determine the Slope of the Trajectory
The slope m of the trajectory at any point is given by the derivative dydx:
dydx=tanθ−gu2cos2θx
This shows that the slope m is a linear function of x.
Step 5: Relate Slope to Time
To express m as a function of time, we substitute x=ucosθ⋅t into the slope equation:
m=tanθ−gu2cos2θ(ucosθ⋅t)
This simplifies to:
m=tanθ−gucosθt
Thus, the slope m varies linearly with time t.
Final Result
The slope m of the trajectory as a function of time t is given by:
m(t)=tanθ−gucosθt
The particle is projected with an initial speed u at an angle θ. We can break this motion into horizontal and vertical components:
- Horizontal component of velocity: ux=ucosθ
- Vertical component of velocity: uy=usinθ
For horizontal motion (x-direction):
- There is no acceleration, so the position as a function of time is given by:
x=uxt=ucosθ⋅t
For vertical motion (y-direction):
- The vertical position as a function of time is given by:
y=uyt−12gt2=usinθ⋅t−12gt2
We can express time t in terms of x from the horizontal motion equation:
t=xucosθ
y=usinθ(xucosθ)−12g(xucosθ)2
This simplifies to:
y=xtanθ−g2u2cos2θx2
This is the equation of the trajectory.
The slope m of the trajectory at any point is given by the derivative dydx:
dydx=tanθ−gu2cos2θx
This shows that the slope m is a linear function of x.
To express m as a function of time, we substitute x=ucosθ⋅t into the slope equation:
m=tanθ−gu2cos2θ(ucosθ⋅t)
This simplifies to:
m=tanθ−gucosθt
Thus, the slope m varies linearly with time t.
The slope m of the trajectory as a function of time t is given by:
m(t)=tanθ−gucosθt
Similar Questions
A particle is thrown with speed u at an angle α with horizontal from the ground. After how much time, the velocity of particle will make an angle β with horizontal.
View SolutionA particle of mass m is projecte dwilth speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle is projected at an angle θ from ground with speed u (g = 10 m/s2 )
Aif u = 10 m/s and θ=30∘, then time of flight will be 1 secBIf u=10√3m/sandθ=60∘, then time of flight will be 3 sec.Cif u=10√3m/sandθ=60∘, then after 2 sec velocity becomes perpendicular to initial velocity.Dif u = 10 m/s and θ=30∘, then velocity never becomes perpendicular to initial velocity during its flight. - Question 2 - Select One
A heavy particle is projected with a velocity at an acure angle with the horizontal into a uniform gravitational field. The slope of the trajectory of the particle varies as
A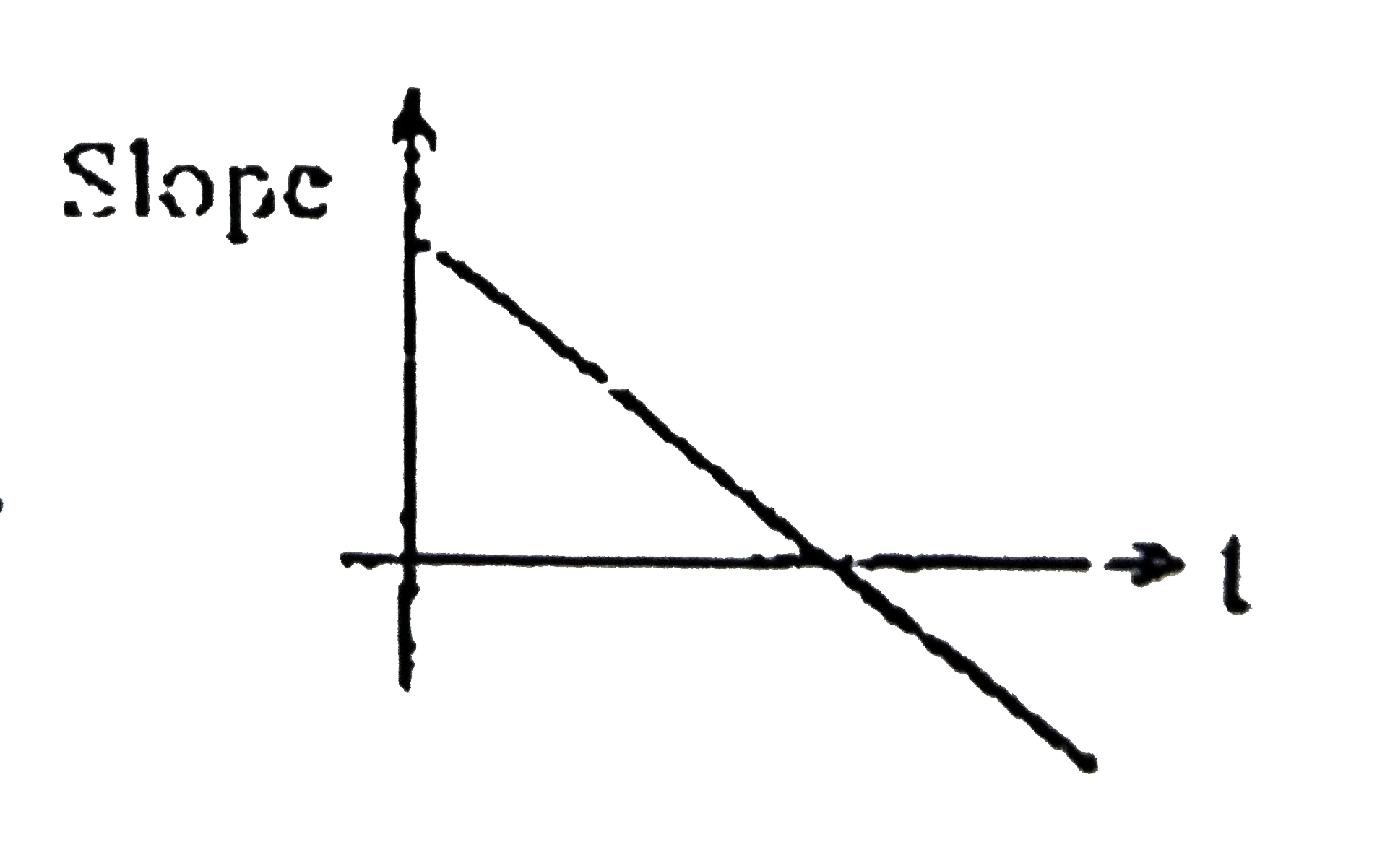 B
B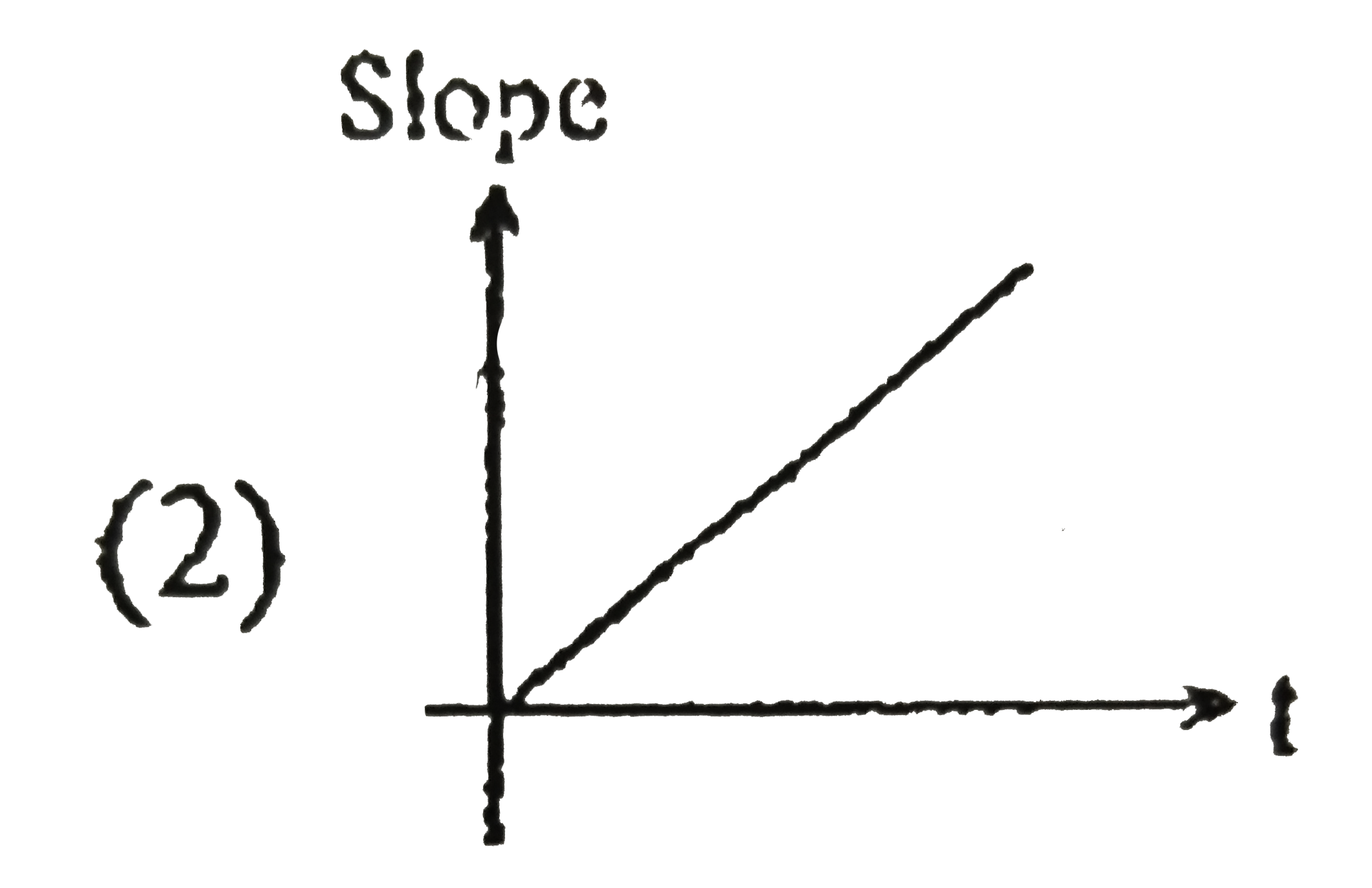 C
C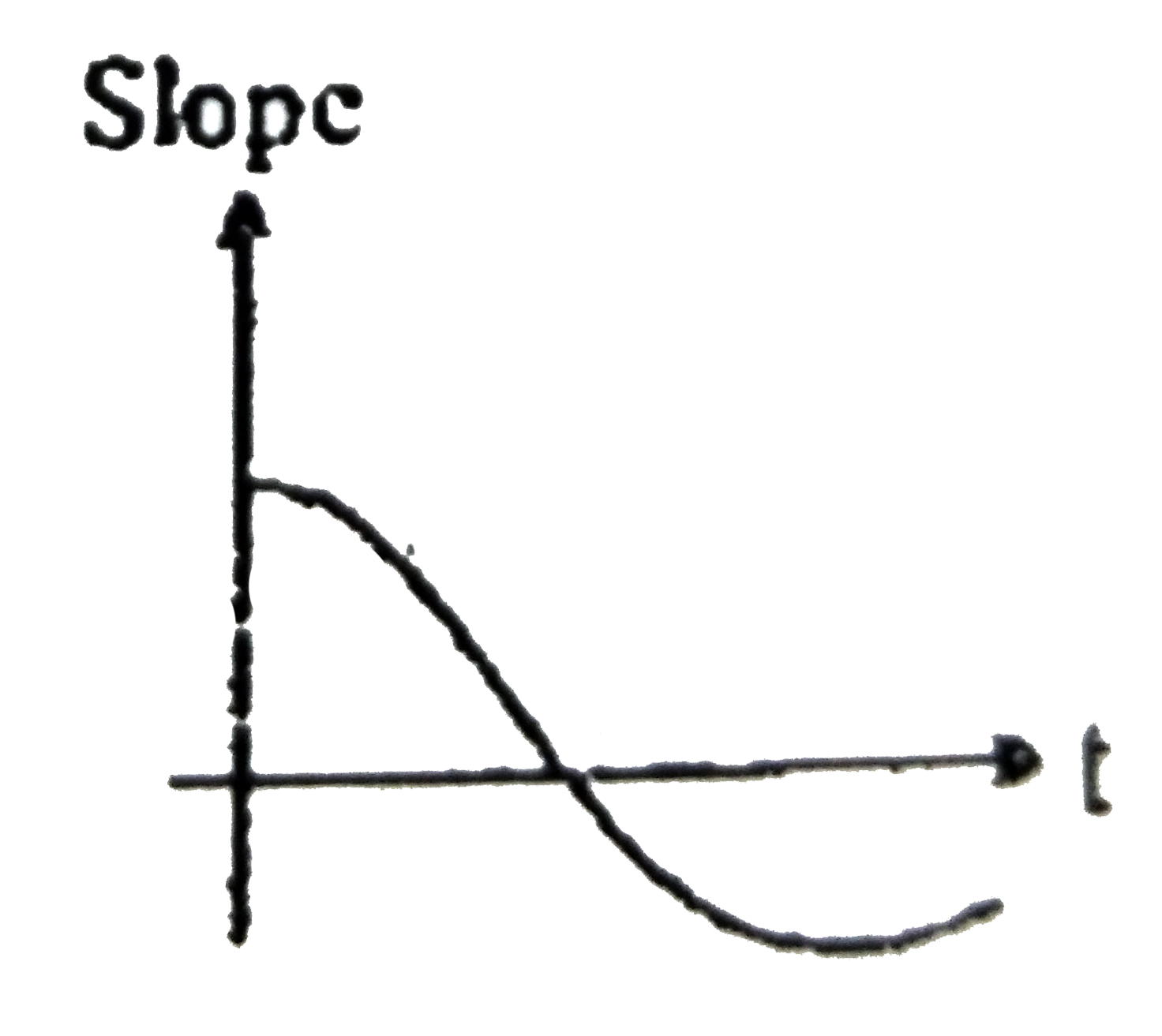 D
D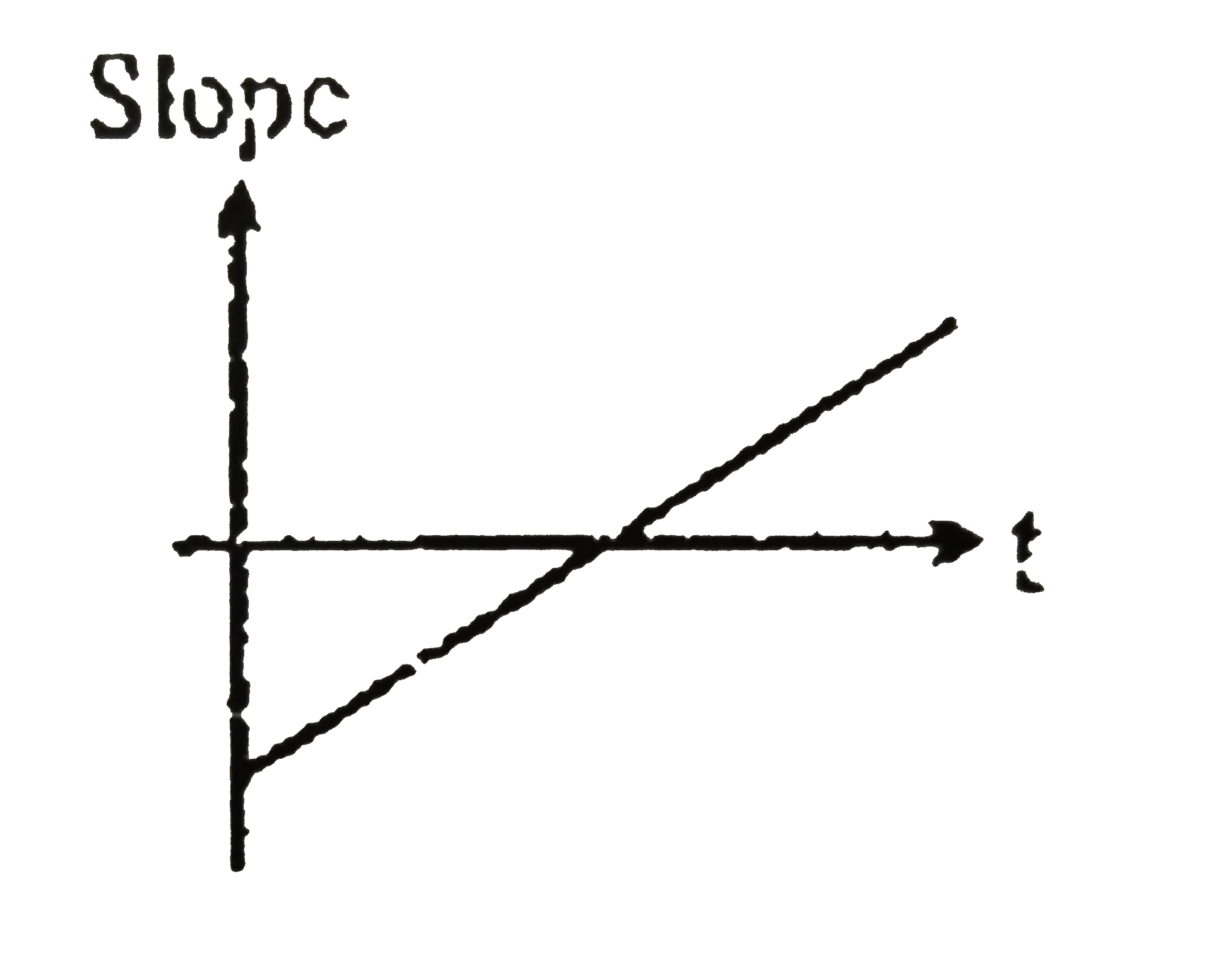
- Question 3 - Select One
A heavy particle is projected with a velocity at an angle with the horizontal into the uniform gravitational field. The slope of the trajectory of the particle varies as
A B
B C
C D
D
A particle is projected with speed u at angle θ with horizontal from ground . If it is at same height from ground at time t1andt2 , then its average velocity in time interval t1 to t2 is
View SolutionA particle of mass m is projected at an angle α to the horizontal with an initial velocity u. The work done by gravity during the time it reaches its highest point is
View SolutionA particle is dropped from a tower in a uniform gravitational field at t=0. The particle is blown over by a horizontal wind with constant velocity. The slope (m) of the trajectory of the particle with horizontal and its kinetic energy vary according to curves. Here, x is the horizontal displacement and h is the height of particle from ground at time t.
View SolutionA particle is projected at an angle θ with the horizontal . If angle of elevation of highest point of trajectory is ϕ when seen from point of projection, then
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View Solution

