A particle is projected with speed u at angle with horizontal from ground . If it is at same height from ground at time , then its average velocity in time interval to is
Zero
u sin
u cos
The correct Answer is:C
To solve the problem, we need to find the average velocity of a particle projected at an angle θ with an initial speed u, when it is at the same height at two different times, t₁ and t₂.
1. Understanding the Motion:
The particle is projected with an initial speed u at an angle θ. The motion can be analyzed in two components: horizontal (x-direction) and vertical (y-direction).
2. Components of Initial Velocity:
- The horizontal component of the initial velocity (u_x) is given by:
ux=ucosθ
- The vertical component of the initial velocity (u_y) is given by:
uy=usinθ
3. Vertical Motion:
The vertical motion is influenced by gravity (g). The vertical position (y) of the particle at any time t can be described by:
y(t)=uyt−12gt2
4. Same Height Condition:
The particle is at the same height at times t₁ and t₂. This means:
y(t1)=y(t2)
Since the vertical motion is symmetrical, the time taken to reach the same height on the way up (t₁) and on the way down (t₂) is such that:
t2=T−t1
where T is the total time of flight.
5. Average Velocity Calculation:
The average velocity (v_avg) over the time interval from t₁ to t₂ is defined as:
vavg=ΔxΔt
where Δx is the change in horizontal position and Δt is the time interval (t₂ - t₁).
6. Horizontal Motion:
The horizontal displacement (x) at any time t is given by:
x(t)=uxt=(ucosθ)t
Thus, the horizontal positions at t₁ and t₂ are:
x(t1)=ucosθ⋅t1
x(t2)=ucosθ⋅t2
7. Change in Horizontal Position:
The change in horizontal position (Δx) is:
Δx=x(t2)−x(t1)=ucosθ(t2−t1)
8. Time Interval:
The time interval (Δt) is:
Δt=t2−t1
9. Substituting into Average Velocity:
Now substituting Δx and Δt into the average velocity formula:
vavg=ucosθ(t2−t1)t2−t1=ucosθ
Final Result:
Thus, the average velocity of the particle in the time interval from t₁ to t₂ is:
ucosθ
The particle is projected with an initial speed u at an angle θ. The motion can be analyzed in two components: horizontal (x-direction) and vertical (y-direction).
- The horizontal component of the initial velocity (u_x) is given by:
ux=ucosθ
- The vertical component of the initial velocity (u_y) is given by:
uy=usinθ
The vertical motion is influenced by gravity (g). The vertical position (y) of the particle at any time t can be described by:
y(t)=uyt−12gt2
The particle is at the same height at times t₁ and t₂. This means:
y(t1)=y(t2)
Since the vertical motion is symmetrical, the time taken to reach the same height on the way up (t₁) and on the way down (t₂) is such that:
t2=T−t1
where T is the total time of flight.
The average velocity (v_avg) over the time interval from t₁ to t₂ is defined as:
vavg=ΔxΔt
where Δx is the change in horizontal position and Δt is the time interval (t₂ - t₁).
The horizontal displacement (x) at any time t is given by:
x(t)=uxt=(ucosθ)t
Thus, the horizontal positions at t₁ and t₂ are:
x(t1)=ucosθ⋅t1
x(t2)=ucosθ⋅t2
The change in horizontal position (Δx) is:
Δx=x(t2)−x(t1)=ucosθ(t2−t1)
The time interval (Δt) is:
Δt=t2−t1
Now substituting Δx and Δt into the average velocity formula:
vavg=ucosθ(t2−t1)t2−t1=ucosθ
Thus, the average velocity of the particle in the time interval from t₁ to t₂ is:
ucosθ
Similar Questions
A particle is projected with a speed v and an angle θ to the horizontal. After a time t, the magnitude of the instantaneous velocity is equal to the magnitude of the average velocity from 0 to t. Find t.
View SolutionA particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View Solution
Knowledge Check
A particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
A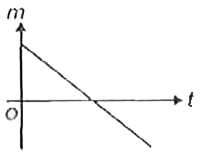 B
B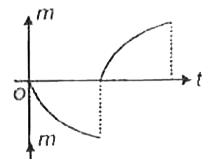 C
C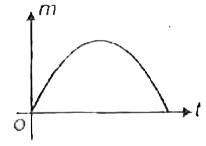 D
D
A particle is projected from ground with speed u and at an angle θ with horizontal. If at maximum height from ground, the speed of particle is 1/2 times of its initial velocity of projection, then find its maximum height attained.
Au2gB2u2gCu22gD3u28gA particle is projected from ground with speed 80 m/s at an angle 30∘ with horizontal from ground. The magnitude of average velocity of particle in time interval t = 2 s to t = 6 s is [Take g = 10 m/s2]
A40√2m/sB40m/sCzeroD40√3m/s
A particle is projected from the ground at t=0 so that on its way it just clears two vertical walls of equal height on the ground. The particle was projected with initial velocity u and at angle θ with the horiozontal. If the particle passes just grazing top of the wall at time t=t1andt=t2, then calculate.
(a) the height of the wall.
(b) the time t1andt2 in terms of height of the wall.
Write the expression for calculating the range of this projectile and separation between the walls.
View SolutionIf a projectile is projected with initial speed u and angle θ from horizontal then what will be its average power up to time when it will hit the ground again ?
View SolutionThe question given below consist of an assertion and the reason . Use the following key to choose appropriate answer:
Assertion : A particle is projected with some speed at a certain angle with the horizontal at time t=0. During the motion , let →v1&→v2 be the velocities of v body at time t1andt2 respectively . In this case →v2−→v1t2−t1 remains constant for any interval of motion .
Reason : At the highest point velocity of the projectile is zero .
View SolutionParticle is projected from the ground at a certain angle with horizontal . If particle takes time T to hit the ground again , then maximum height of the projectile is
View SolutionParticle A is projected with speed u at an angle θ with the horizontal . Another particle B is also projected with same speed u at an angle 90−θ with the horizontal . Both the projectiles are fired from the ground and reaches the ground after completing the projectile . Time of flight for A is tA and that for B it is tB. Range of the projectile A is RA and that for B is RB . Maximum height reached by the projectile A is hA and that for B is hB

View Solution
