Question

Consider function $f\left(x\right)={\sin }^{-1}\left(\sin x\right)+{\cos }^{-1}\left(\cos x\right),x\in [0,2\pi ]$
(a) Draw the graph of $y=f\left(x\right)$
(b) Find the range of $f\left(x\right)$
(c) Find the area bounded by $y=f\left(x\right)$ and x-axis

Answer

Range is `[0,pi]`, Area `= pi^(2)` sq. units

Explanation

`f(x) = sin^(-1) (sin x) + cos^(-1) (cos x)`
`{:(= x + x = 2x,x in [0, pi//2]),(= pi - x + x = pi,x in [pi//2, pi]),(= pi - x + 2 pi - x = 3pi - 2x,x in [pi, 3 pi//2]),(= x - 2pi + 2pi - x = 0,x in [3 pi//2, 2 pi]):}`
Graph of the function is as shown in the following figure

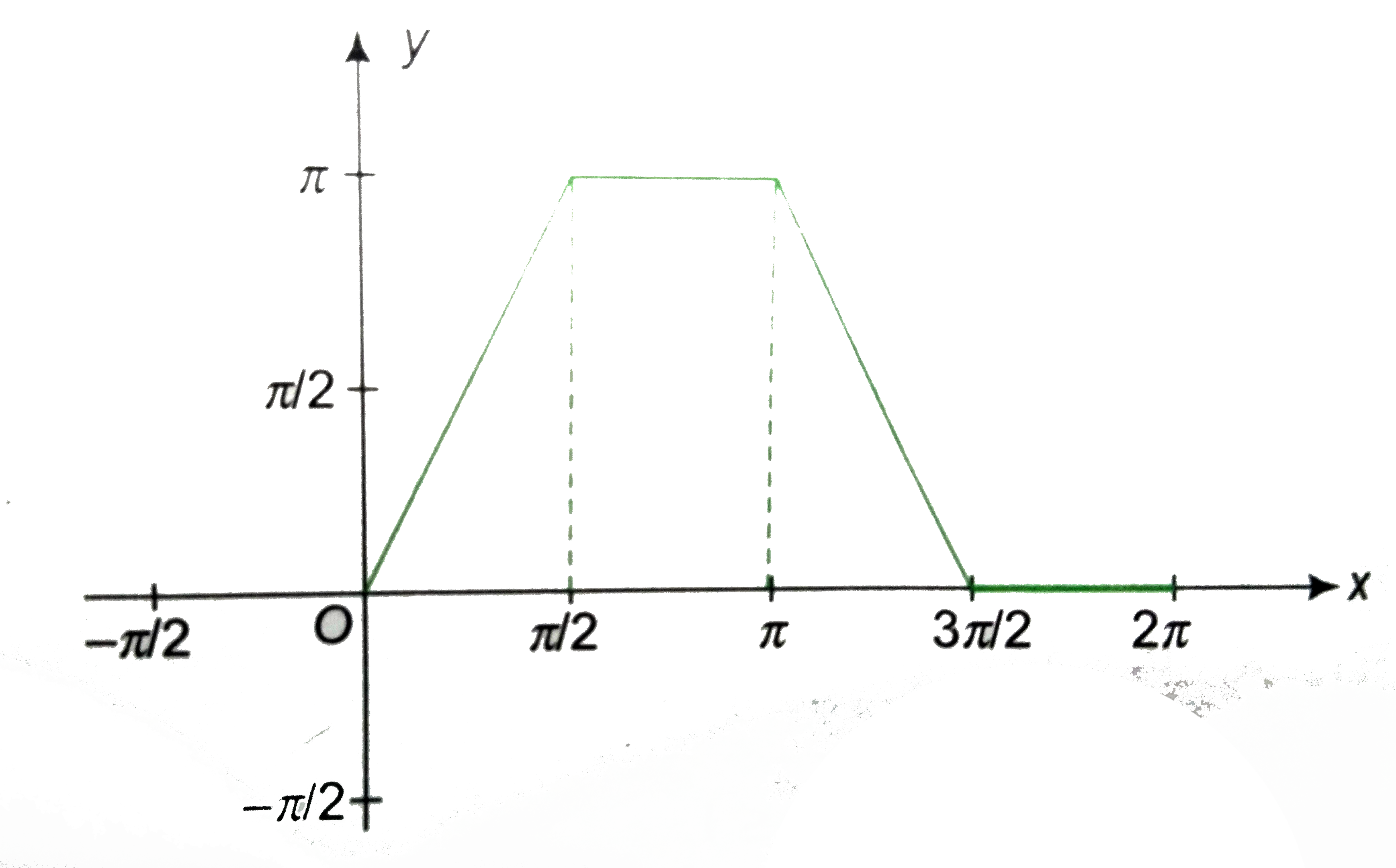
From the graph, rangle is `[0, pi]`
Also, area bounded by `y = f (x)` and x -axis is,
`A = (1)/(2) ((3pi)/(2) + (pi)/(2)) (pi)`
`pi^(2)` sq. units