The equation $3 {cos}^{- 1} x - π x - \frac{π}{2} = 0$ has

A

one negative solution

B

one positive solution

C

no solution

D

more than one solution

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$3 {cos}^{- 1} x - π x - \frac{π}{2} = 0 or {cos}^{- 1} x = \frac{π x}{3} + \frac{π}{6}$

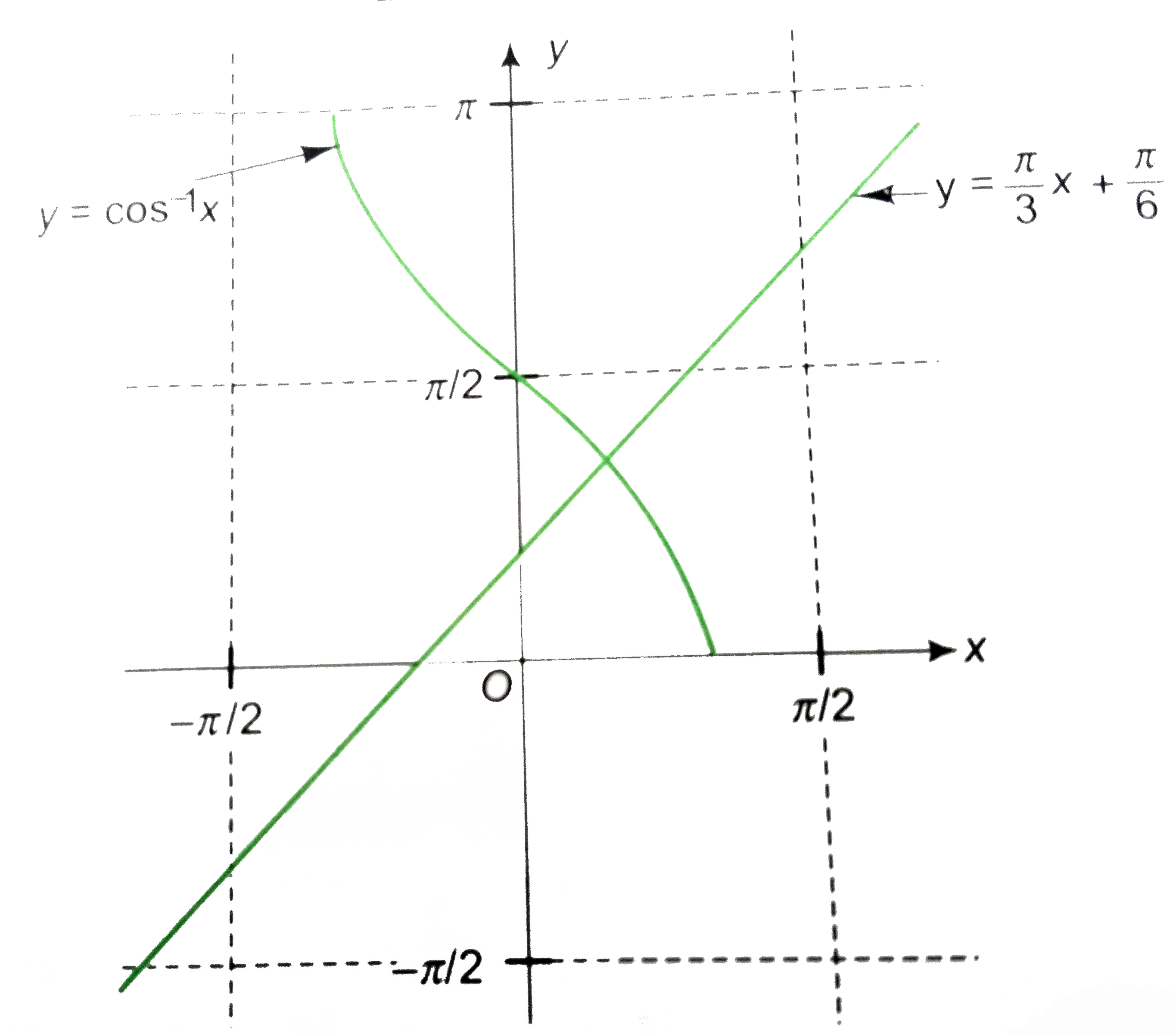
From the graph, there is only one solution

|

Updated on:21/07/2023

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Multiple)
24videos
INVERSE TRIGONOMETRIC FUNCTIONS
BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Comprehension)
16videos
INVERSE TRIGONOMETRIC FUNCTIONS
BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.6
9videos
INVERSE TRIGONOMETRIC FUNCTIONS
BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year
20videos
INTRODUCTION TO VECTORS
BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9videos
JEE 2019

Similar Questions

Knowledge Check

Question 1 - Select One
$3 {cos}^{- 1} x - π / x - π / 2 = 0$ for
Aone solution
Bone and only one solution
Cno solution
Dmore than one solution
Question 2 - Select One
The number of solutions of the equation ${cos}^{2} (\frac{π}{3} cos x - \frac{8 π}{3}) = 1$ in the interval $[0, 10 π]$ is
A1
B3
C5
D7
Question 3 - Select One
The solution of the equation ${cos}^{- 1} x + {cos}^{- 1} 2 x = \frac{2 π}{3}$ is
A $x = \pm \frac{\sqrt{3}}{\sqrt{28}}$
B $x = \pm \frac{\sqrt{3}}{\sqrt{26}}$
C $x = \pm \frac{1}{\sqrt{2}}$
D $x = \pm \frac{\sqrt{3}}{\sqrt{38}}$

CENGAGE-INVERSE TRIGONOMETRIC FUNCTIONS-Exercise (Single)

Home
Ask Doubt
Profile