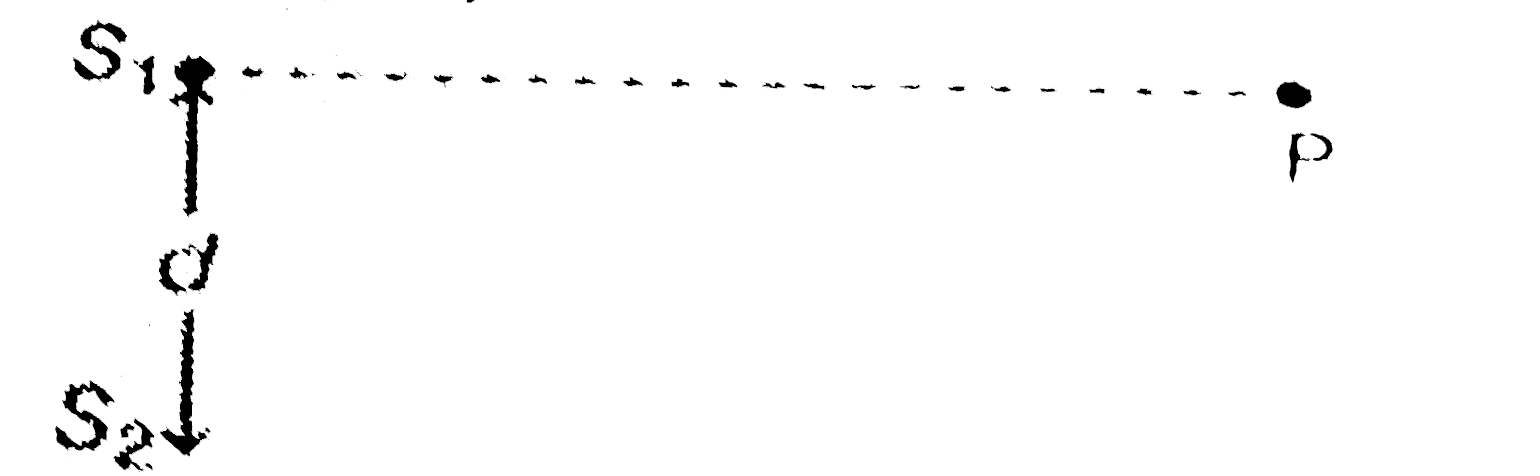
Consider two coherent monochromatic (wavelength λ) sources S1andS2 separated by a distance d. The ratio of intensity of S1 and that of S2 at point P is 4. The distance of P from S1 if the resultant intensity at point P is equal to 94, times the intensity due to S1 is : (n is a positive integer )
d2−n2λ22nλ
d2+n2λ22nλ
nλd√d2−n2λ2
2nλd√d2−n2λ2
The correct Answer is:A
Topper's Solved these Questions
- WAVE OPTICSBOOK - DC PANDEYCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced B. More than one option is correct
5 Videos
- WAVE OPTICSBOOK - DC PANDEYCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced C. Comprehension Type Questions. Passage (I)
2 Videos
- WAVE OPTICSBOOK - DC PANDEYCHAPTER - WAVE OPTICSEXERCISE - For JEE main (Only one option is Correct )
22 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEYCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER
22 Videos
Similar Questions
Consider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
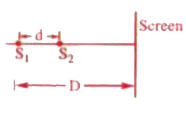
View SolutionTwo coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View Solution
Knowledge Check
Consider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
Ad2−n2λ22nλBd2+n2λ22nλCnλd√d2−n2λ2D2nλd√d2−n2λ2Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circlesTwo coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
 Astraigth linesBsemi-circleCconcentric circlesDpoints
Astraigth linesBsemi-circleCconcentric circlesDpoints
Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
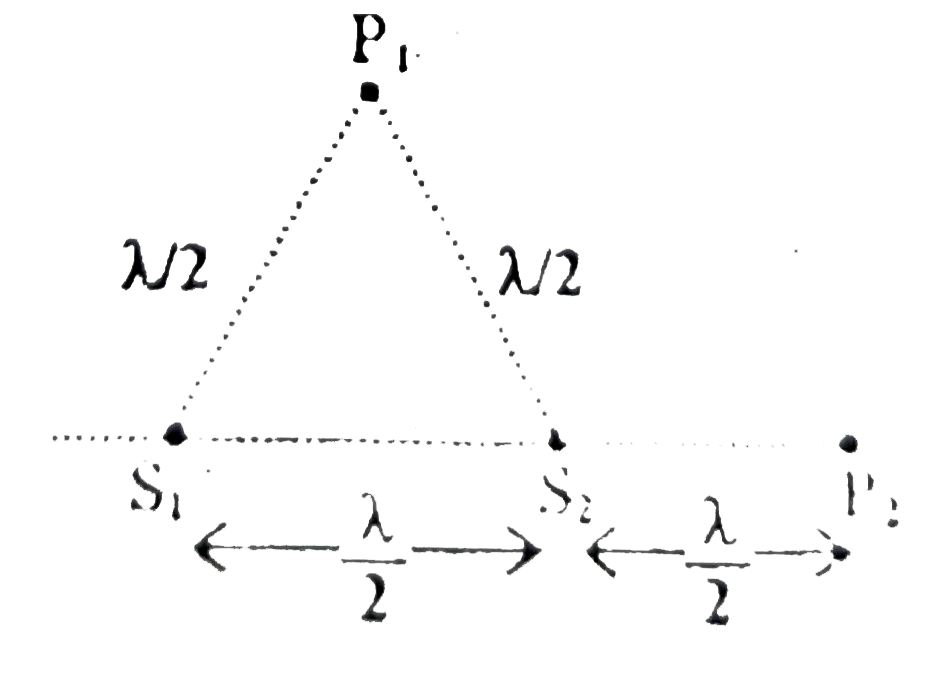
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
View Solution
