In any triangle ABC, prove that $A B^{2} + A C^{2} = 2 (A D^{2} + B D^{2})$ , where D is the midpoint of BC.

Video Solution

Text Solution

Verified by Experts

Let point B and C lie on the x-axis such that $B D = D C$ , where, $D (0, 0)$ is midpoint of BC.
Let point A be (x,y).

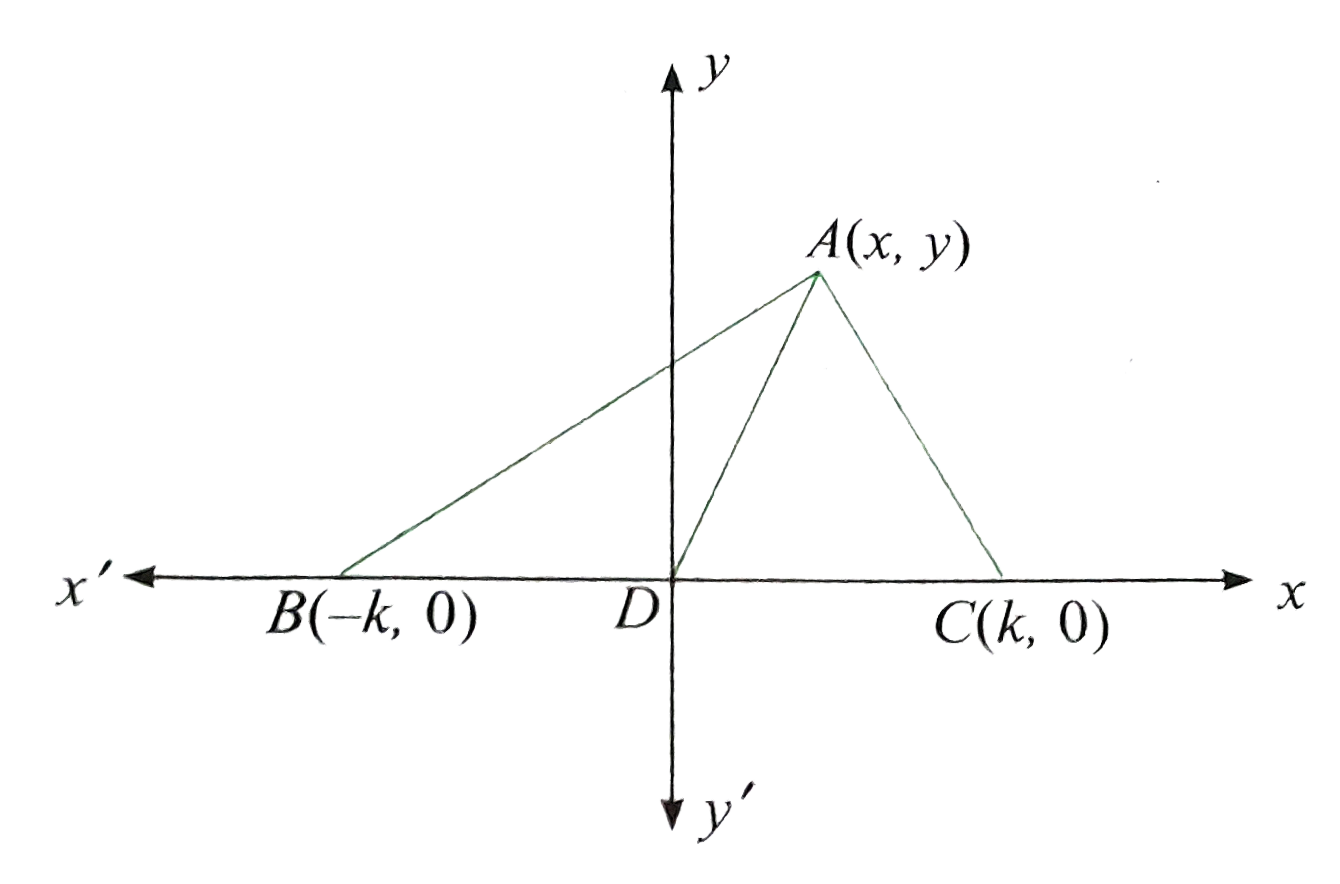
$B D = k$ .So, point B is $(- k, 0)$ and point C is $(k, 0)$ .
Now, $A B^{2} + A C^{2} = {(x + k)}^{2} + {(y - 0)}^{2} + {(x - k)}^{2} + {(y - 0)}^{2}$
$= x^{2} + k^{2} + 2 x k + y^{2} + x^{2} k^{2} - 2 x k + y^{2}$
$= 2 x^{2} + 2 y^{2} + 2 k^{2} = 2 (x^{2} + y^{2} + k^{2})$
And $2 (A D^{2} + B D^{2}) = 2 [{(x - 0)}^{2} + {(y - 0)}^{2} + k^{2}]$
$= 2 (x^{2} + y^{2} + k^{2})$
Therefore, $A B^{2} + A C^{2} = 2 (A D^{2} + B D^{2})$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a triangle ABC, it is known that AB=AC. Suppose D is the mid-point of AC and BD=BC=2. Then the area of the triangle ABC is-
A2
B $2 \sqrt{2}$
C $\sqrt{7}$
D $2 \sqrt{7}$

CENGAGE-COORDINATE SYSYEM -JEE Main Previous Year

Home
Ask Doubt
Profile