Orthocenter and circumcenter of a $Delta A B C$ are $(a, b) a n d (c, d)$ , respectively. If the coordinates of the vertex $A$ are $(x_{1}, y_{1}),$ then find the coordinates of the middle point of $B C .$

Video Solution

Text Solution

Verified by Experts

Given are the orthocentre $H (a, b)$ and the circumcentre $O (c, d)$ .

$∴$ Centroid, $G = (\frac{2 c + a}{2 + 1}, \frac{2 d + b}{2 + 1}) \equiv (\frac{2 c + a}{3}, \frac{2 d + b}{3})$

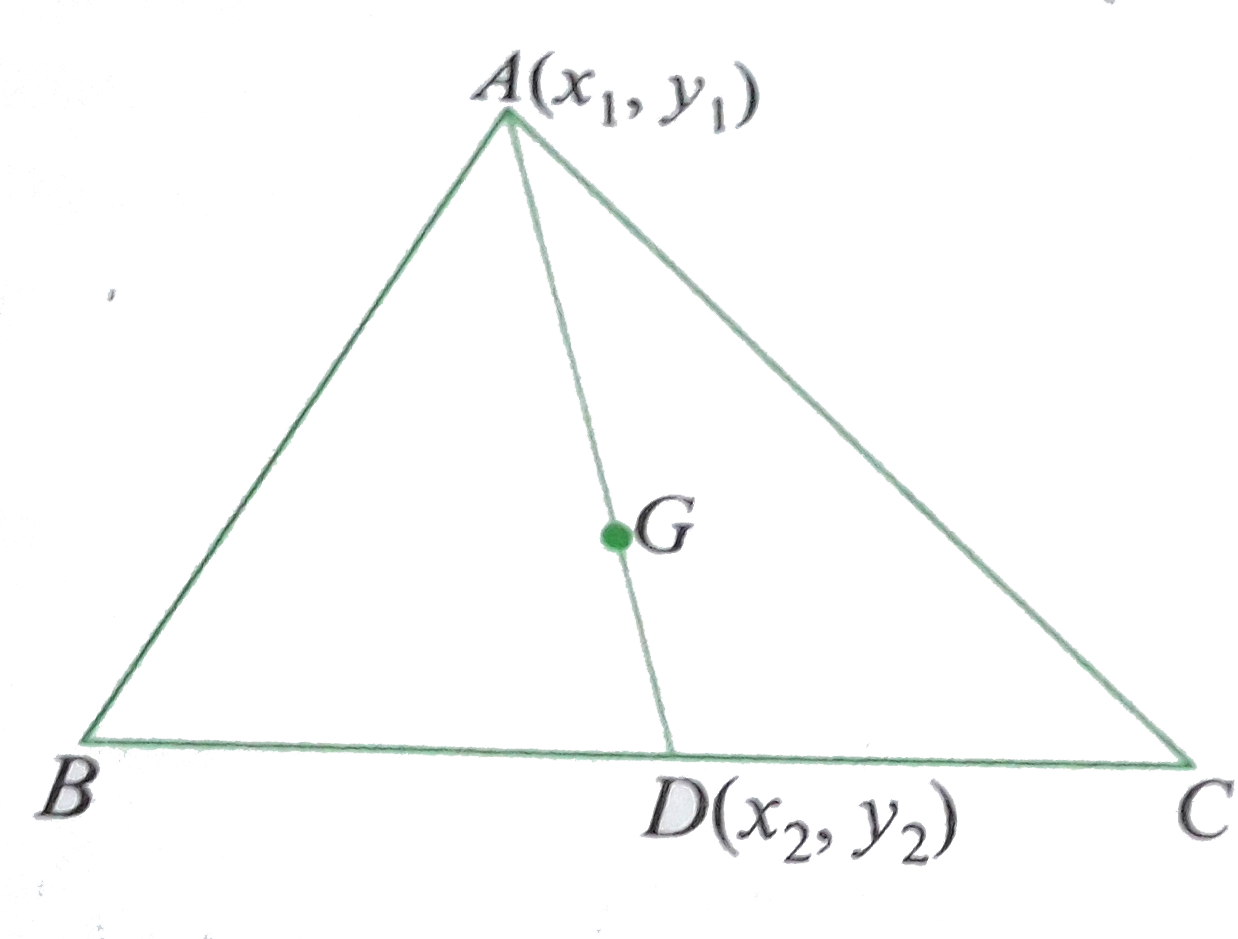
Now, centroid G divides AD in the ratio $2 :$ , where D is the midpoint of BC.
$∴ \frac{2 c + a}{3} = \frac{2 x_{2} + x_{1}}{3}$
and $\frac{2 d + b}{3} = \frac{2 y_{2} + y - 1}{3}$
$∴ x_{2} = \frac{2 c + a - x_{1}}{2}, y_{2} = \frac{2 d + b - y_{1}}{2}$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(-2,7), the coordinates of vertex A can be
A(1,6)
B $(- 1 / 2, 5)$
C $(- 5 / 6, 6)$
Dnone of these
Question 2 - Select One or More
ABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(-2,7), the coordinates of vertex A can be
A $(1, 6)$
B $(- \frac{1}{2}, 5)$
C $(\frac{5}{6}, 6)$
D $(- 7, \frac{1}{8})$
Question 3 - Select One
If the coordinates of the centroid and a vertex of an equilaterqal triangle are (1,1) and (1,2) respectively, then the coordinates of another vertex, are
A $(\frac{2 - \sqrt{3}}{2}, - \frac{1}{2})$
B $(\frac{2 + 3 \sqrt{3}}{2}, - \frac{1}{2})$
C $(\frac{2 + \sqrt{3}}{2}, - \frac{1}{2})$
Dnone of these

CENGAGE-COORDINATE SYSYEM -JEE Main Previous Year

Home
Ask Doubt
Profile