The vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
Video Solution
Text Solution
The angle bisector of ∠B meets the opposite side in D.
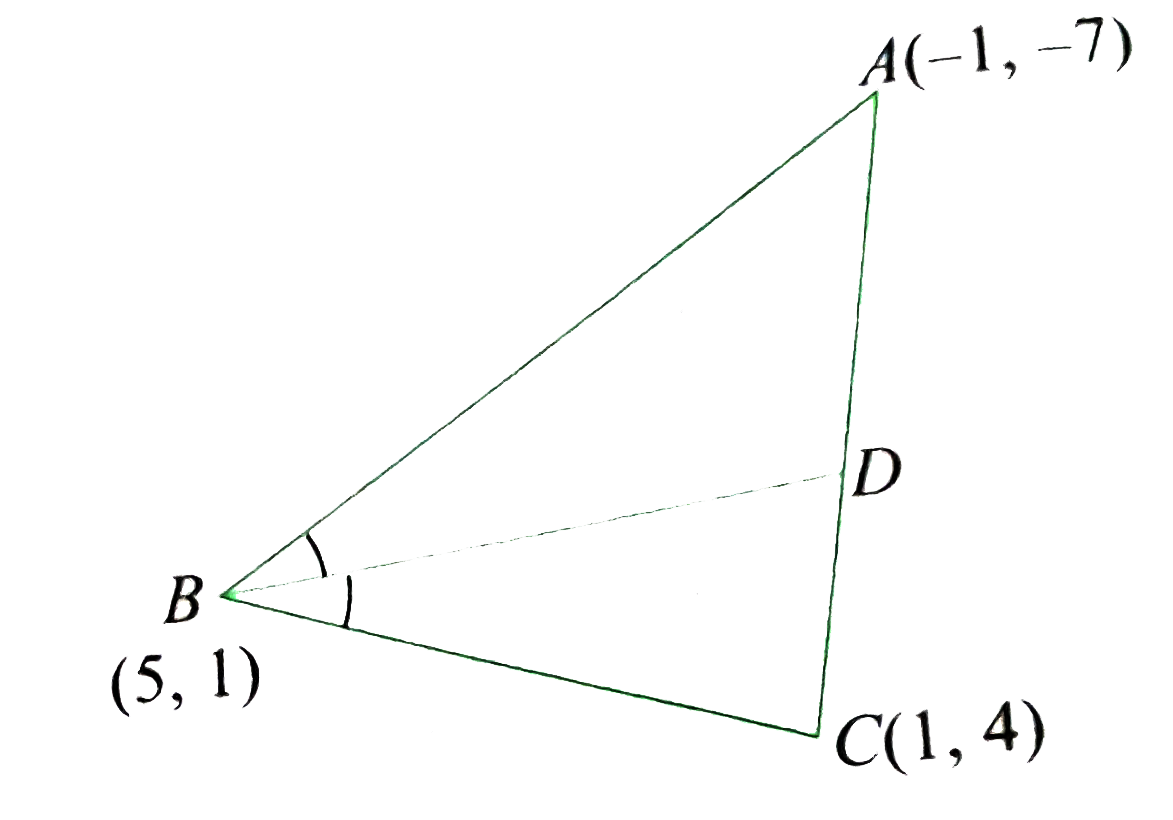
Using angle bisector theorem , we have
AD:DC=AB:BC
Now, AB=√(5+1)2+(1+7)2=10
and BC=√(5−1)2+(1−4)2=5
∴D=(2(1)+1(−1)2+1,2(4)+1(−7)2+1)=(13,13)
∴BD=√(5−13)2+(1−13)2=10√23
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.16videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.28videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Knowledge Check
- Question 1 - Select One
The vertices of a triangle are (A(−1,−7),B(5,1), and C(1,4). The equation of the bisector of ∠ABC is____
Ax + 7y - 2 = 0Bx - 7y - 2 = 0Cx - 7y + 2 = 0DNone of these - Question 2 - Select One
The vertices of a triangle are A(−1,−7), B(5,1) and C(1,4). The equation of the internal bisector of the angle ∠ABC is
A3x−7y−8=0Bx−7y+2=0C3x−3y−7=0DNone of these - Question 3 - Select One
The vertices of a triangle are A(3, 7), B(3, 4) and C(5,4). The equation of the bisector of ∠ABC is
AY = x+1By=x-1Cy=3x-5DY=4
The vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). The equation of the bisector of the angle ABC
View SolutionThe vertices of a triangle are A(5,4,6),B(1,−1,3)and(4,3,2). The internal bisector of ∠BACmeets BC in D. Find AD.
View SolutionThe vertices of a triangle are A(1,1,2), B (4,3,1) and C (2,3,5). The vector representing internal bisector of the angle A is
View SolutionThe vertices f the triangle are A(5,4,6), B(1,−1,3)nad C(4,3,2). The internal bisector of angle A meets BC at D. Find the coordinates of D and the length AD.
View SolutionThe vertices of a triangle are A(1, 1, 2), B(4, 3, 1) and C(2, 3, 5). A vector representing the internal bisector of the angle A is
View Solution

