If the points $(a, 0), (b, 0), (0, c)$ , and $(0, d)$ are concyclic $(a, b, c, d > 0)$ , then prove that $a b = c d$ .

Video Solution

Text Solution

Verified by Experts

Without loss of generality, assume that $b > a and d > c$ . SinceABCD is cyclic quadrilateral, sum of oppsite angles is $180^{\circ}$ .

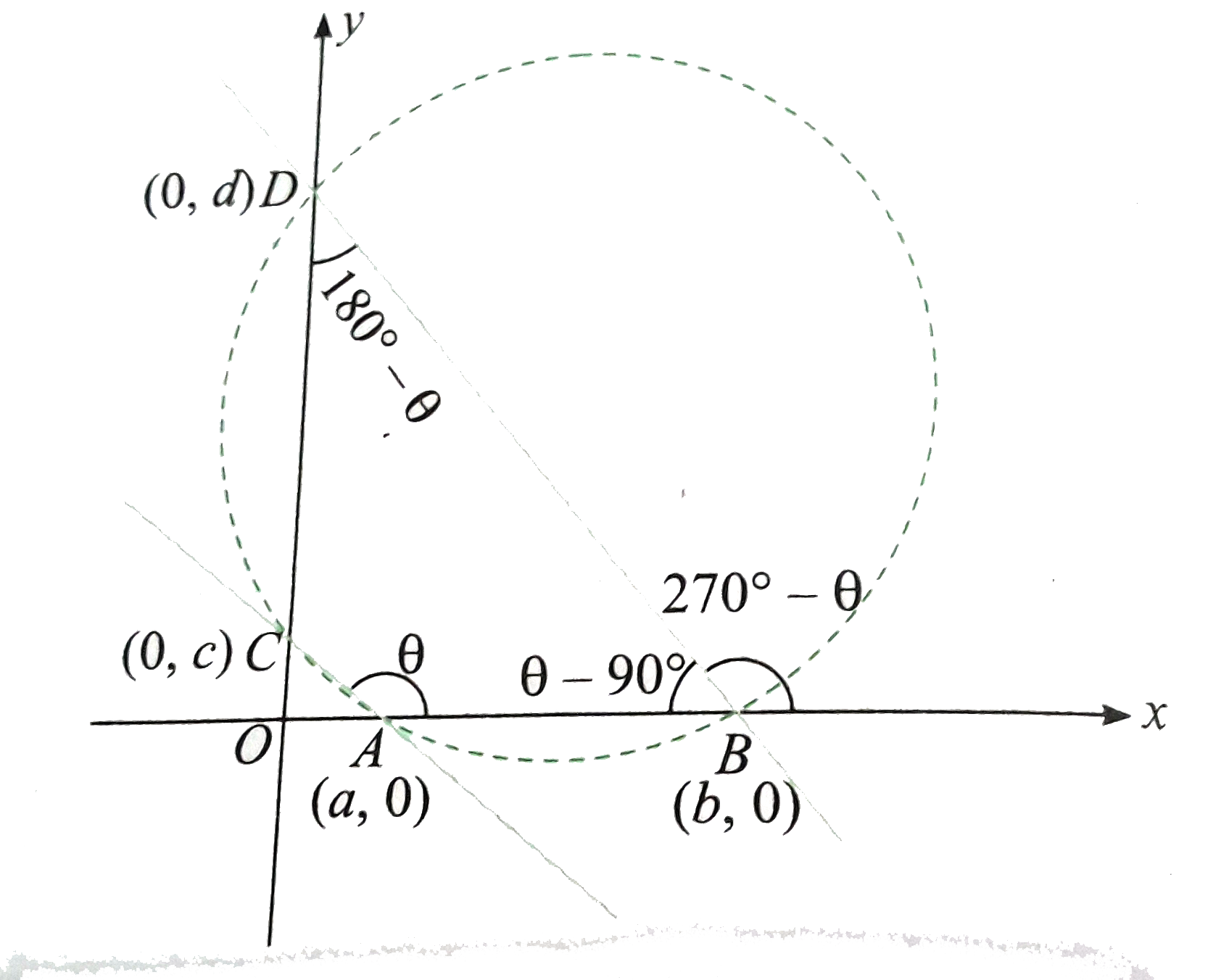
i.e., $∠ B A C + ∠ C D B = 180^{\circ}$
Let $∠ B A C = θ$ (=inclination of line AC)
$∴ ∠ C D B = 180^{\circ} - θ$
Therefore, inclination of line BD is $270^{\circ} - θ$ slope of line AC.
$tan θ = - \frac{c}{a}$
Slope of $B D, tan (270^{\circ} - θ) = - \frac{d}{b}$
or $cot θ = - \frac{d}{b}$
From (1) and (2), we get
$(tan θ) (cot θ) = (- \frac{c}{a}) (- \frac{d}{b})$
or $a b = c d$

Updated on:21/07/2023