Question

For a given point A(0,0), ABCD is a rhombus of side 10 units where slope of AB is ${\displaystyle \frac{4}{3}}$and slope of AD is ${\displaystyle \frac{3}{4}}$. The sum of abscissa and ordinate of point C (where C lies in first quadrant) is

Answer

`B(6,8),C(14,14),D(8,6)`

Explanation

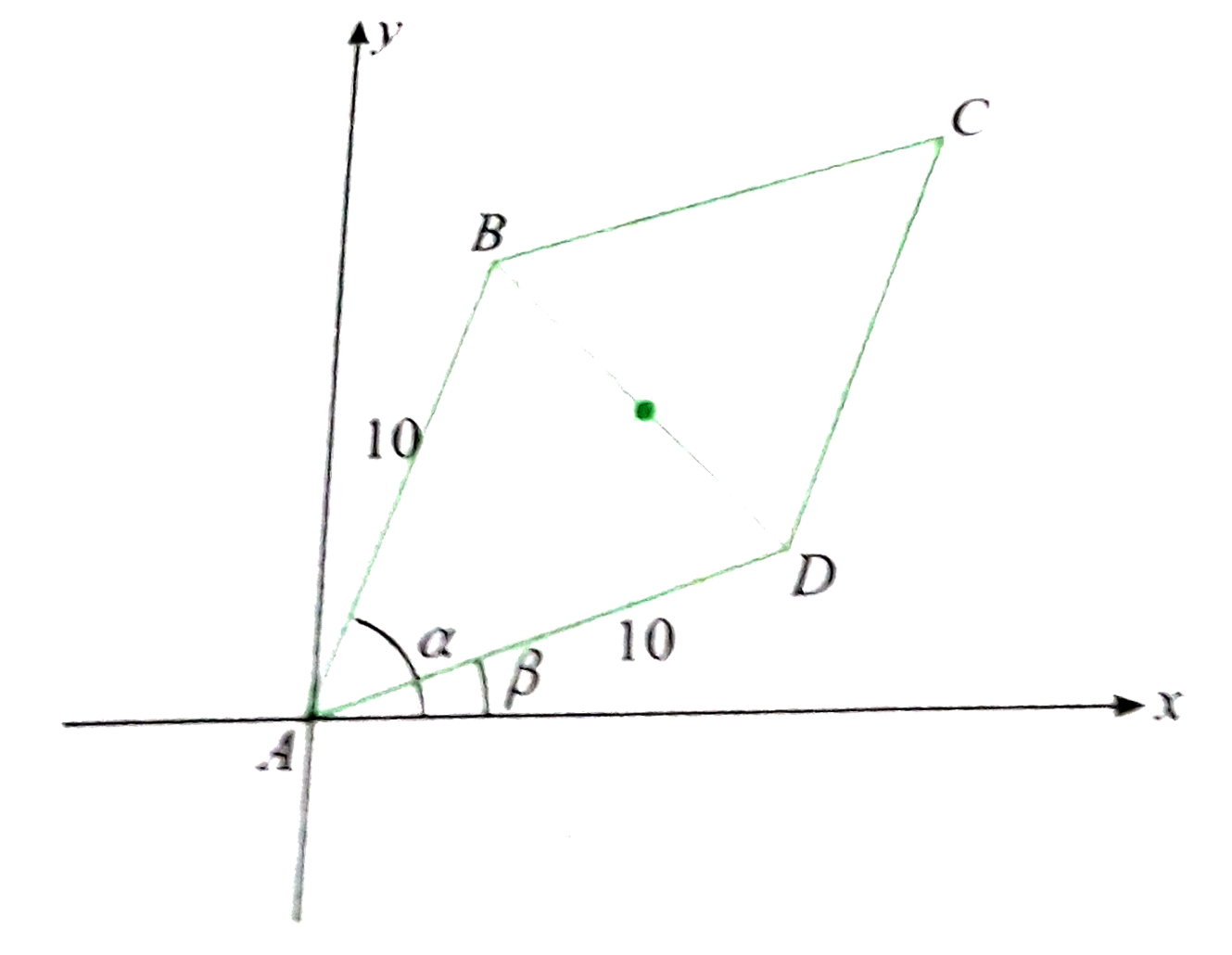
In the figure,`tan alpha=(4)/(3)`
`therefore` Coordinates of point B
`-=(10cosalpha,10sinalpha)`
`-=(10xx(3)/(5),10xx(4)/(5))-=(6,8)`
Also, `tanbeta=(3)/(4)`
`therefore` coordinates of Point D
`-=(10cosbeta,10sinbeta)`
`-=(10xx(4)/(5),10xx(3)/(5))-=(8,6)`
Diagonals of rhombus bisect. So, midpoint of BD is `(7,7)` which is midpoint of AC. therefore, coordinates of C are `(14,14)`.