The medians AD and BE of the triangle with vertices $A (0, b), B (0, 0)$ and $C (a, 0)$ are mutually perpendicular. Prove that $a^{2} = 2 b^{2}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:NA

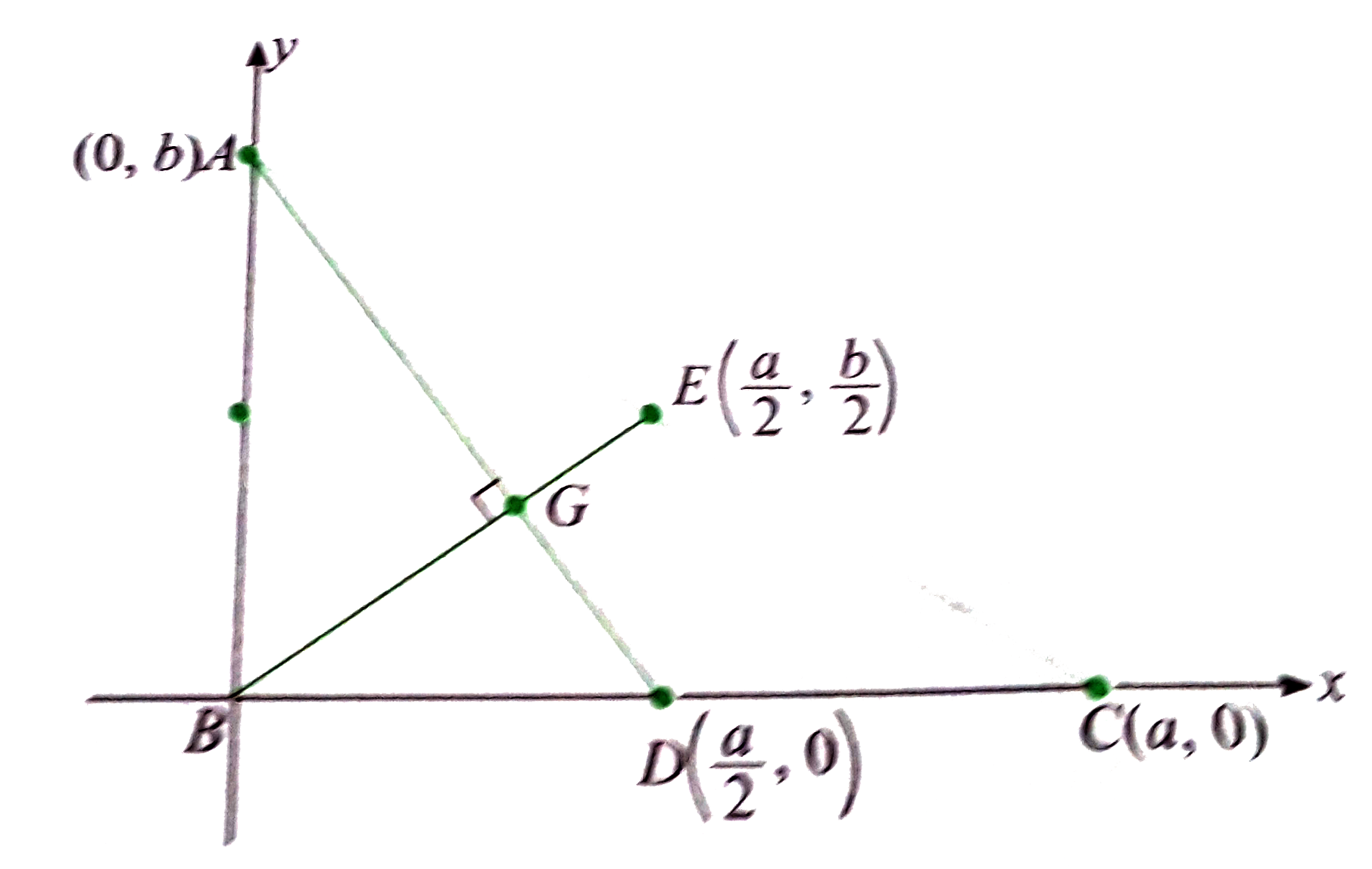
From the figure,
Slope of $B E, m_{B E} = \frac{b}{a}$
Slope of $A D, m_{A D} = - \frac{2 b}{a}$
Given that AD and BE are perpendicular.
$∴ m_{B E} \times m_{A D} = - \frac{2 b^{2}}{a^{2}} = - 1$
$\Rightarrow a^{2} = 2 b^{2}$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
The medians AD and BE of the triangle with vertices A(0,b),B(0,0) and C(a,0) are mutually perpendicular if
A $b = \sqrt{2} a$
B $a = \sqrt{2} b$
C $b = - \sqrt{2} a$
D $a = - \sqrt{2} b$
Question 2 - Select One or More
The medians AD and BE of the triangle with vertices A(0, b), B(0, 0) and C(a, 0) are mutually perpendicular if
A $b = a \sqrt{2}$
B $a = b \sqrt{2}$
C $b = - a \sqrt{2}$
D $a = - b \sqrt{2}$
Question 3 - Select One
If the medians PT and RS of a triangle with vertices P (0, b), Q (0, 0) and R (a, 0) are perpendicular to each other, which of the following satisfies the relationship between a and b?
A $4 b^{2} = a^{2}$
B $2 b^{2} = a^{2}$
C $a = - 2 b$
D $a^{2} + b^{2} = 0$

CENGAGE-COORDINATE SYSYEM -Exercise 1.4

Home
Ask Doubt
Profile