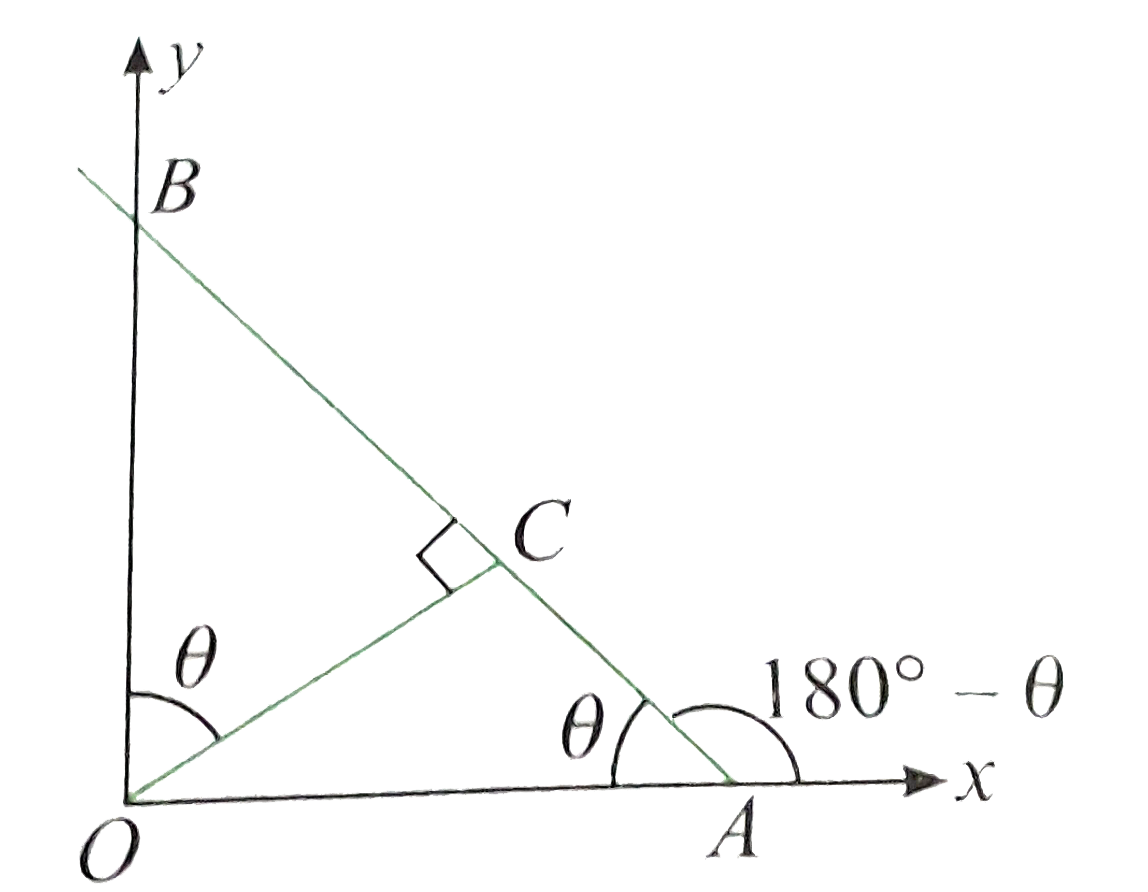
The foot of the perpendicular on the line $3 x + y = λ$ drawn from the origin is $C .$ If the line cuts the $x$ and the y-axis at $A a n d B$ , respectively, then $B C : C A$ is $1 : 3$ (b) $3 : 1$ (c) $1 : 9$ (d) $9 : 1$

A

$1 : 3$

B

$3 : 1$

C

$1 : 9$

D

$9 : 1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

${tan 180}^{\circ} - θ) =$ Slope of $A B = - 3$
$∴ tan θ = 3$
$∴ \frac{O C}{A C} = tan θ, \frac{O C}{B C} = cot θ$
or $\frac{B C}{A C} = \frac{tan θ}{cot θ} = {tan}^{2} θ = 9$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The foot of the perpendicular drawn from the origin to a plane is the point $(1, - 3, 1)$ . What is the intercept cut on the x-axis by the plane ?
A1
B3
C $\sqrt{11}$
D11
Question 2 - Select One
The foot of the perpendicular drawn from the origin on the line $3 x + y = λ (λ \neq 0)$ is P. If the line meets x-axis at A and y-axis at B, then the ratio $B P : P A$ is:
A $9 : 1$
B $1 : 3$
C $3 : 1$
D $1 : 9$
Question 3 - Select One
The foot of the perpendicular from $(2, 4 - l)$ to the line $x + 5 = \frac{1}{4} (y + 3) = - \frac{1}{9} (z - 6)$ is
A $(- 4, 1, - 3)$
B $(4, - 1, - 3)$
C $(- 4, - 1, 3)$
D $(- 4, - 1, - 3)$

CENGAGE-COORDINATE SYSYEM -Exercise (Single)

Home
Ask Doubt
Profile