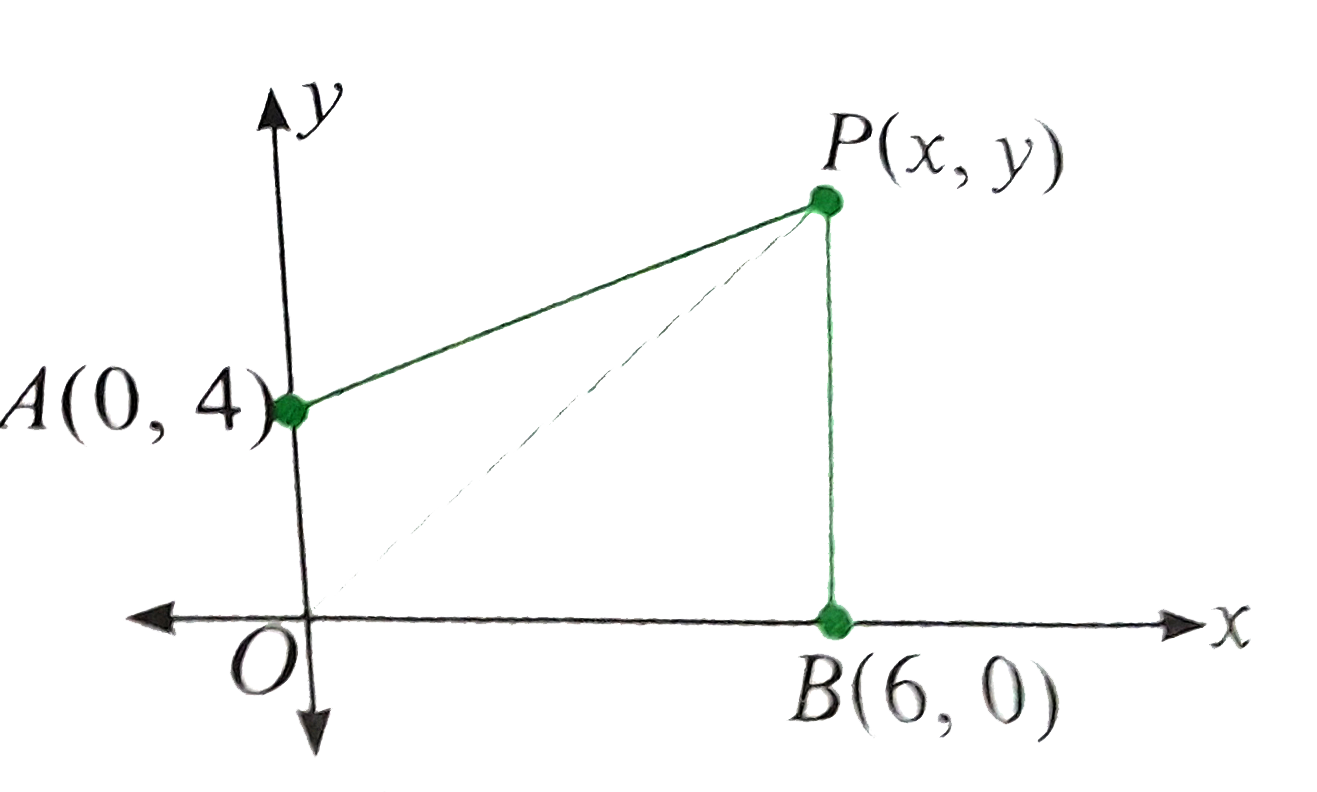
Let $0 \equiv (0, 0), A \equiv (0, 4), B \equiv (6, 0) .$ Let $P$ be a moving point such that the area of triangle $P O A$ is two times the area of triangle $P O B$ . The locus of $P$ will be a straight line whose equation can be $x + 3 y = 0$ (b) $x + 2 y = 0$ $2 x - 3 y = 0$ (d) $3 y - x = 0$

A

$x + 3 y = 0$

B

$x + 2 y = 0$

C

$2 x - 3 y = 0$

D

$3 y - x = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, D

Let point P be (x,y).
$a r Δ P O A = \frac{1}{2} (O A) | x | = 2 | x |$
$a r Δ P O A = \frac{1}{2} (O B) | y | = 3 | y |$
$∴ 2 | x | = 6 | y |$
or $| x | = 3 | y |$ or $3 y - x = 0 or 3 y + x 0$

Updated on:21/07/2023

|

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area of triangle formed by the straight lines whose equations are $y = 4 x + 2, 2 y = x + 3$ and $x = 0$ is :
A $\frac{25}{7 \sqrt{2}}$
B $\frac{\sqrt{2}}{28}$
C $\frac{1}{28}$
D $\frac{15}{7}$

CENGAGE-COORDINATE SYSYEM -Exercise (Multiple)

Home
Ask Doubt
Profile