O is the origin and B is a point on the x-axis at a distance of 2 units from the origin. Match the following lists. 
The correct Answer is:a top;btop,s;ctop,r;dtoq,s
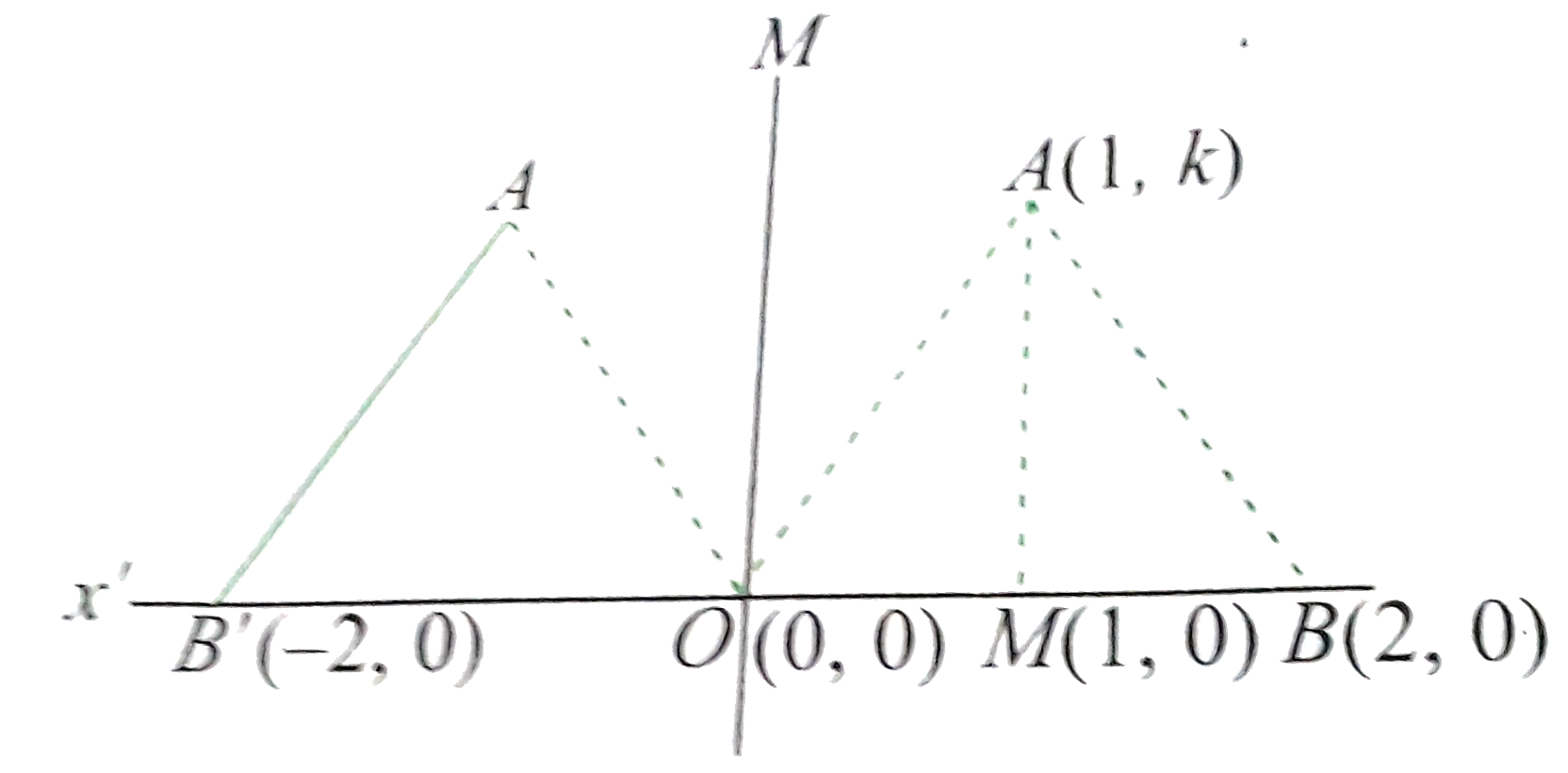
From the figure , is equilateral. Hence,
i.e., (for first quadrant)
or (for fourth quadrant)
then the possible coordinates are .
Similarly , for the second quadrant, the point is and for the third quadrant , the point is .
(b) Case i :
If , then , Therefore
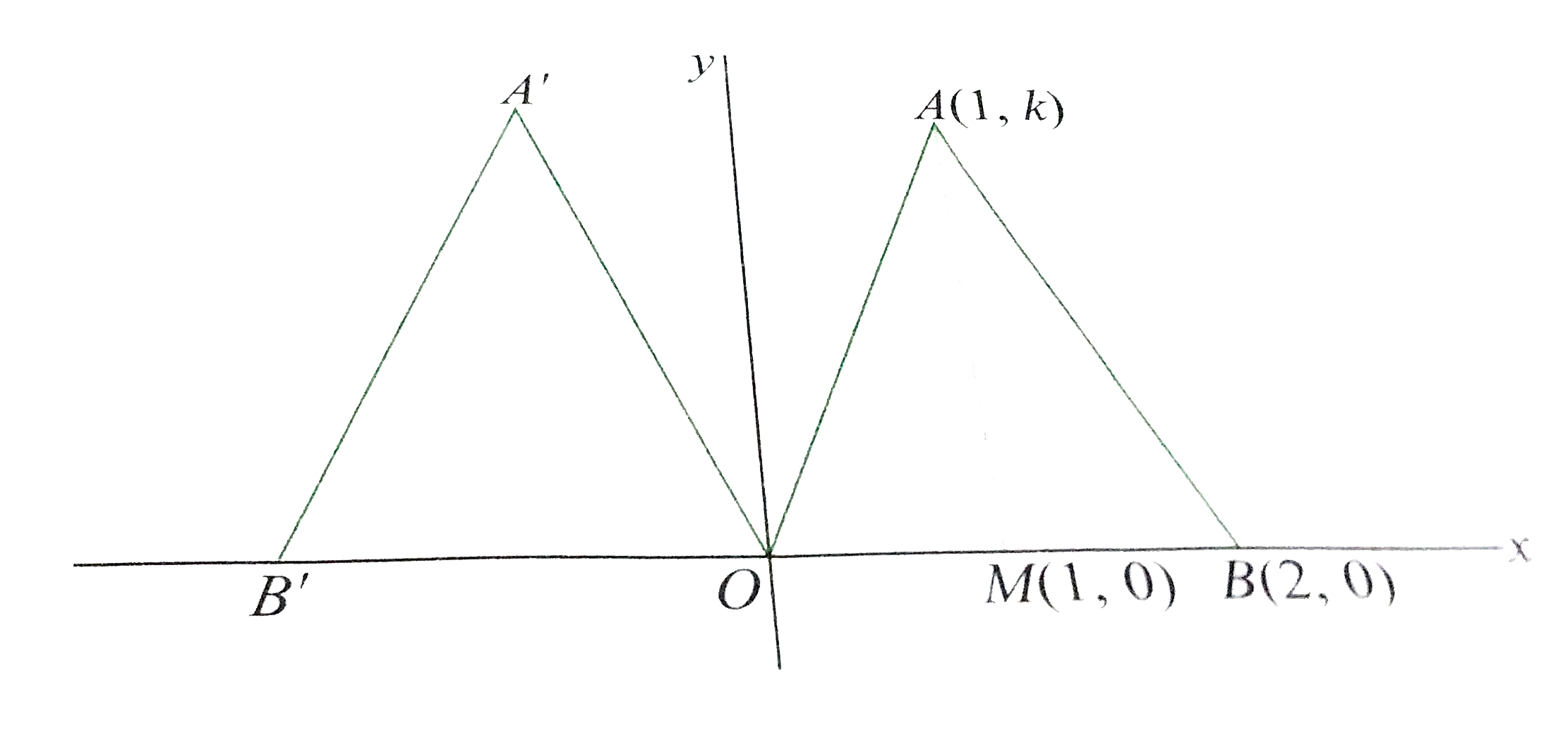
Hence, point A is . By symmetry, all possible points are .
Case ii:
and
Hence, point A is , By symmetry, all possible points are .
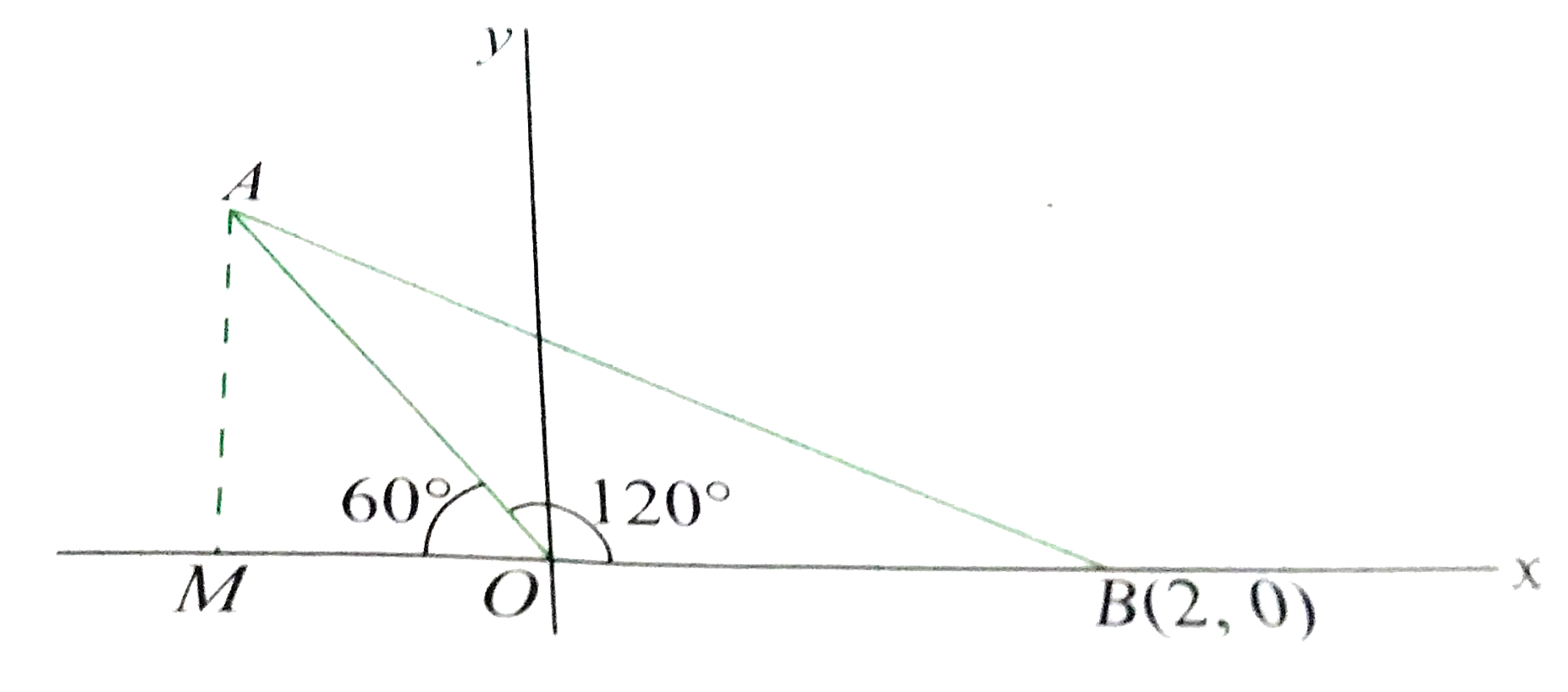
(c). 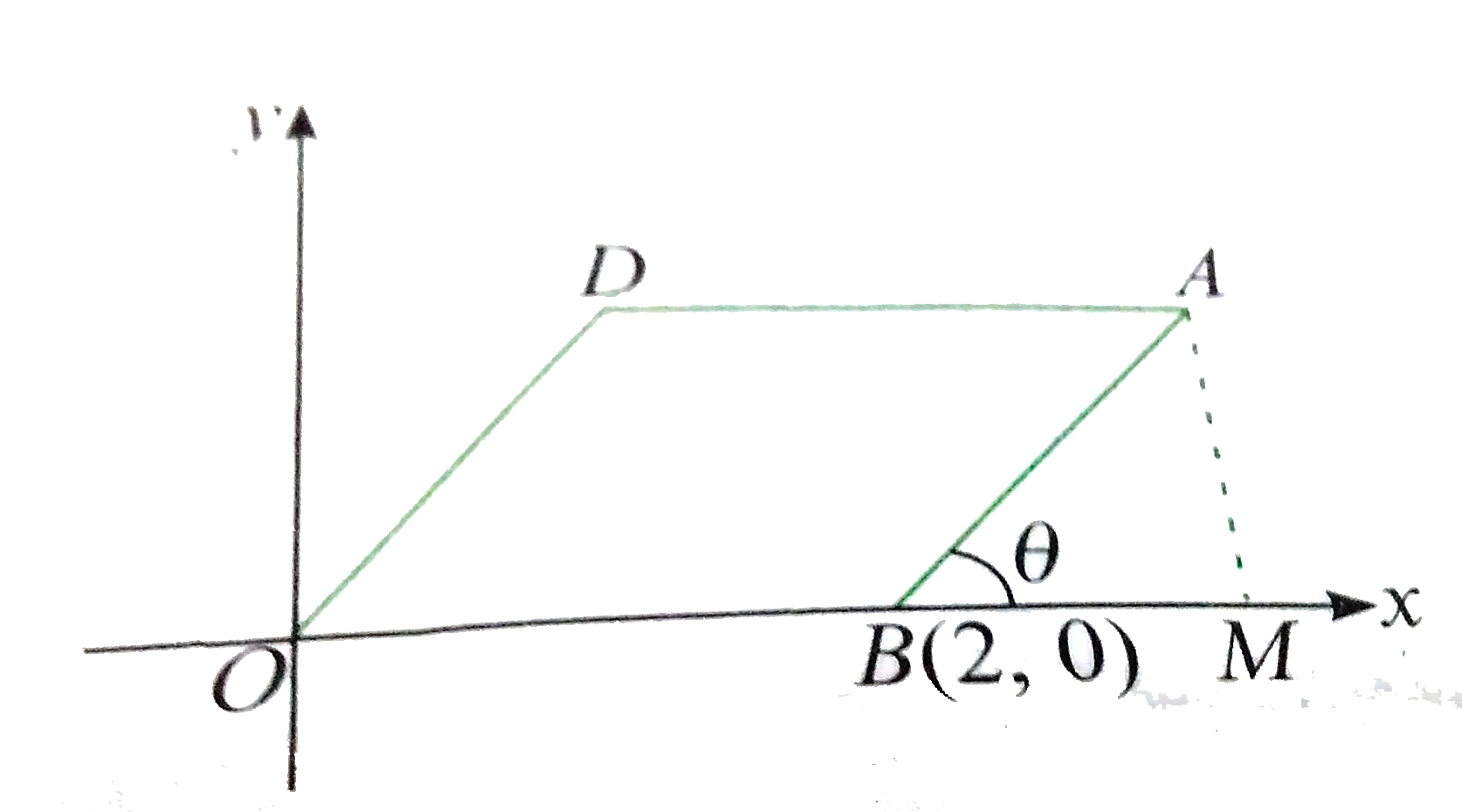
Let .
Area of
or
or
or
Hence, A has coordinates , By symmetry, all the possible coordinates are .
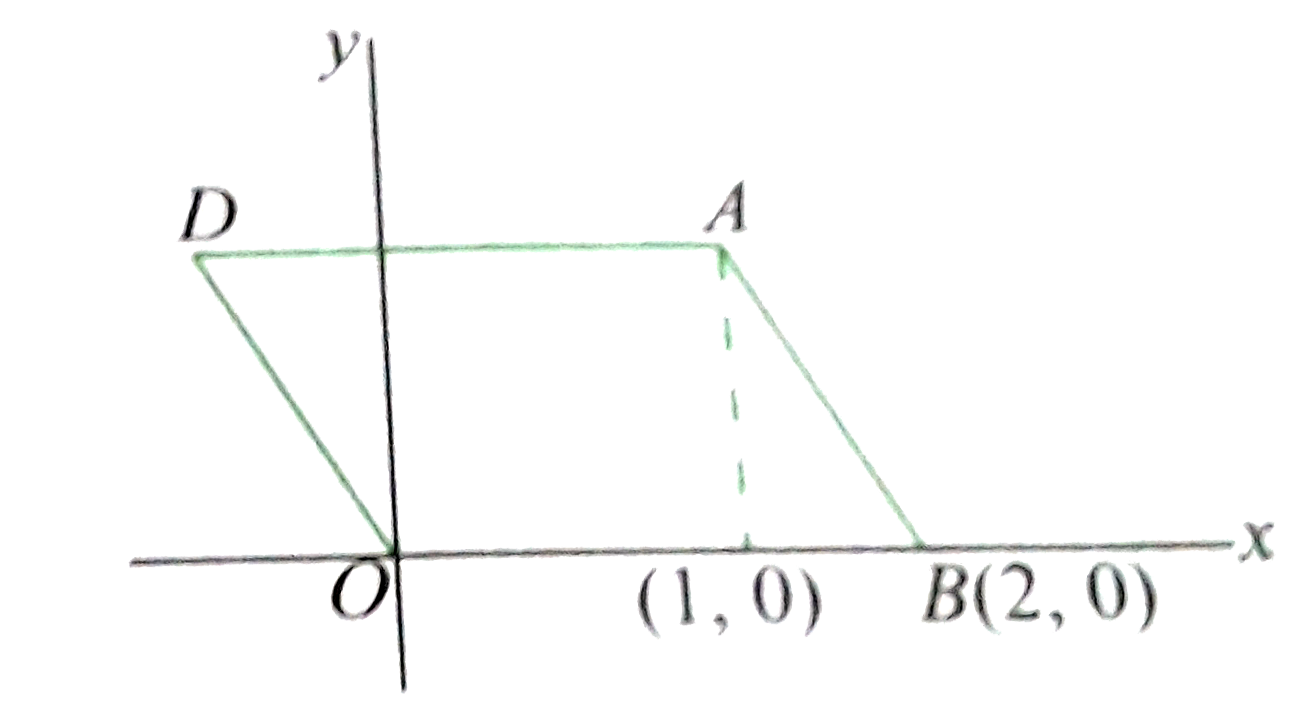
From the figure, A has coordinates .
By symmetry, all possible coordinates are .
(d) 
or
In ,
Since is isosceles, point A lies on the perpendicular bisector of OB. Therefore,
Hence, the coordinates of A will be in the first quadrant. By symmetry, all possible coordinates of A are .
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Numerical)
12 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main Previous Year
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Comprehension)
10 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Knowledge Check
A is a point on the positive x-axis at a distance 3 units from the origin and B is a point on the positive y-axis at a distance 4 units from the origin. If P divides AB in the ratio 1 : 2, the coordinates of P are
A(1, 8/3)B(2, 4/3)C(8/3, 1)D(4/3, 2)O is the origin and P is point at a distance of 3 units from origin. If direction ratios of OP are <1,−2,−2>, then the coordinates of P are
A(1,−2,−2)B(3,−6,−6)C(13,−23,−23)D(19,−29,−29)
9.The graph of x=3 is a line
a) Parallel to x axis at a distance of 3 units from the origin.
b) Parallel to y axis at a distance of 3 units from the origin.
c) Makes an intercept 3 on x axis.
d) Makes an intercept 3 on y axis
View SolutionFind the equation of a circle which touches y-axis at a distance of 2 units from the origin and cuts an intercept of 3 units with the positive direction of x-axis
View SolutionGraph of y=6 is a line:
(a) parallel to x-axis at a distance 6 units from the origin.
(b) parallel to y-axis at a distance 6 units from the origin.
(c) making an intercept 6 on the x-axis.
(d) making an intercept 6 on both the axis.
View SolutionGraph of y=6 is a line:
(a) parallel to x-axis at a distance 6 units from the origin.
(b) parallel to y-axis at a distance 6 units from the origin.
(c) making an intercept 6 on the x-axis.
(d) making an intercept 6 on both the axis.
View SolutionGraph of y=6 is a line:
(a) parallel to x-axis at a distance 6 units from the origin.
(b) parallel to y-axis at a distance 6 units from the origin.
(c) making an intercept 6 on the x-axis.
(d) making an intercept 6 on both the axis.
View SolutionGraph of y=6 is a line:
(a) parallel to x-axis at a distance 6 units from the origin.
(b) parallel to y-axis at a distance 6 units from the origin.
(c) making an intercept 6 on the x-axis.
(d) making an intercept 6 on both the axis.
View Solution
