If lines $2 x - 3 y + 6 = 0$ and $k x + 2 y = 12 = 0$ cut the coordinate axes in concyclic points, then the value of $| k |$ is

Video Solution

Text Solution

Verified by Experts

The correct Answer is:3

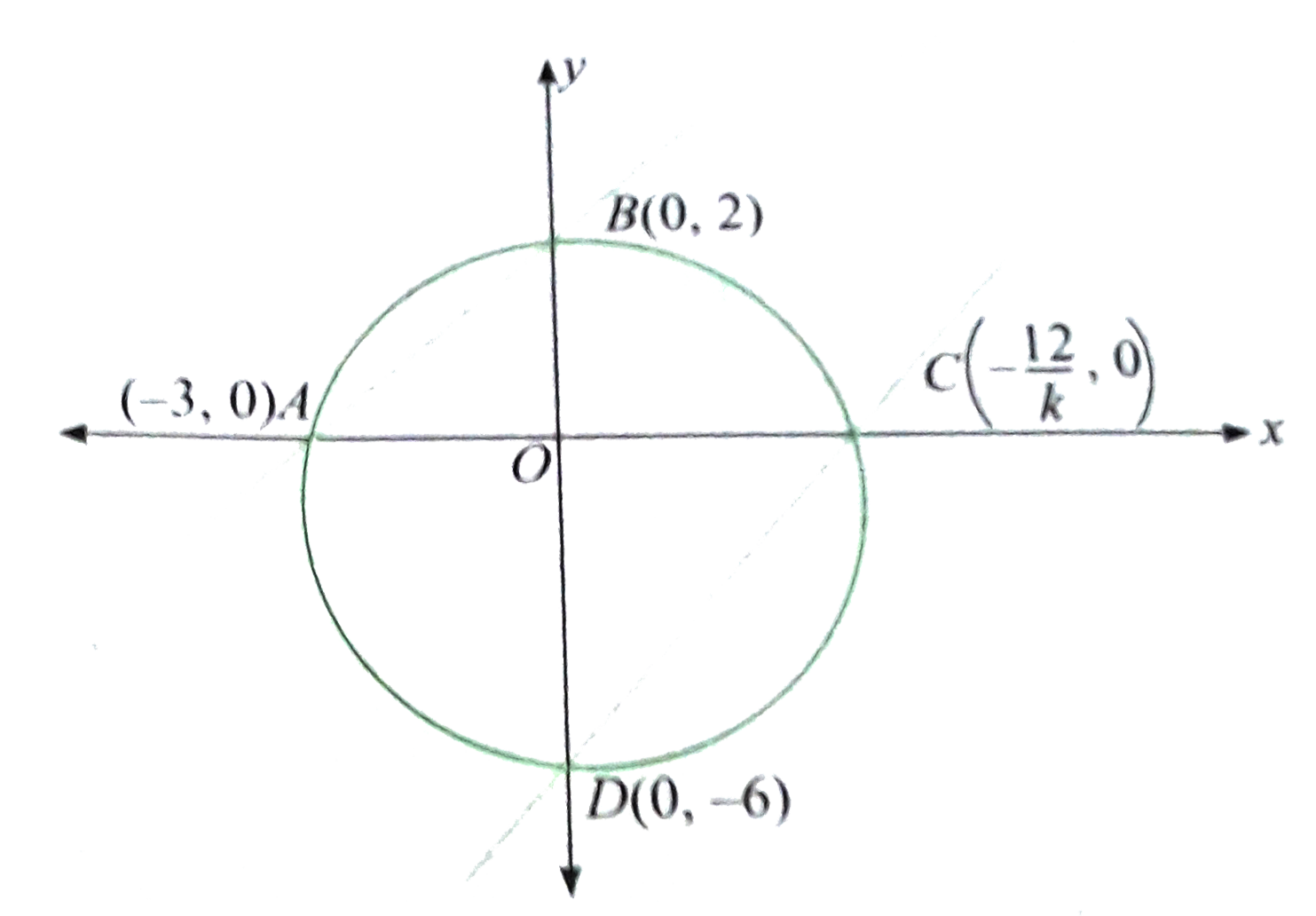
$2 x - 3 y + 6 = 0$ meets the axes at $A (- 3, 0)$ and $B (0, 2)$ . $k x + 2 y + 12 = 0$ meets the axes at $D (0, - 6)$ and $C (- 12 / k, 0)$ , Points A,B.C and D will be concyclic, if
$O A \times O C = O B \times O D$
$\Rightarrow 3 \times (- 12 / k) = 2 \times 6$
$\Rightarrow k = - 3$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $2 x + 3 y - 6 = 0$ and $9 x + 6 y - 18 = 0$ cuts the axes in concyclic points, then the centre of the circle, is
A(2, 3)
B(3, 2)
C(5, 5)
D(5/2, 5/2)
Question 2 - Select One
If the lines $a_{1} x + b_{1} y + c_{1} = 0$ and $a_{2} x + b_{2} y + c_{2} = 0$ cut the coordinate axes in concyclic points, then
A $a_{1} a_{2} = b_{1} b_{2}$
B $a_{1} b_{1} = a_{2} b_{2}$
C $a_{1} / a_{2} = b_{1} / b_{2}$
Dnone

CENGAGE-COORDINATE SYSYEM -Exercise (Numerical)

Home
Ask Doubt
Profile