A particle is projected from the ground so as to graze the four upper vertices of a regular hexagor, whose side is 2a and which is placed vertically with one side on the ground.
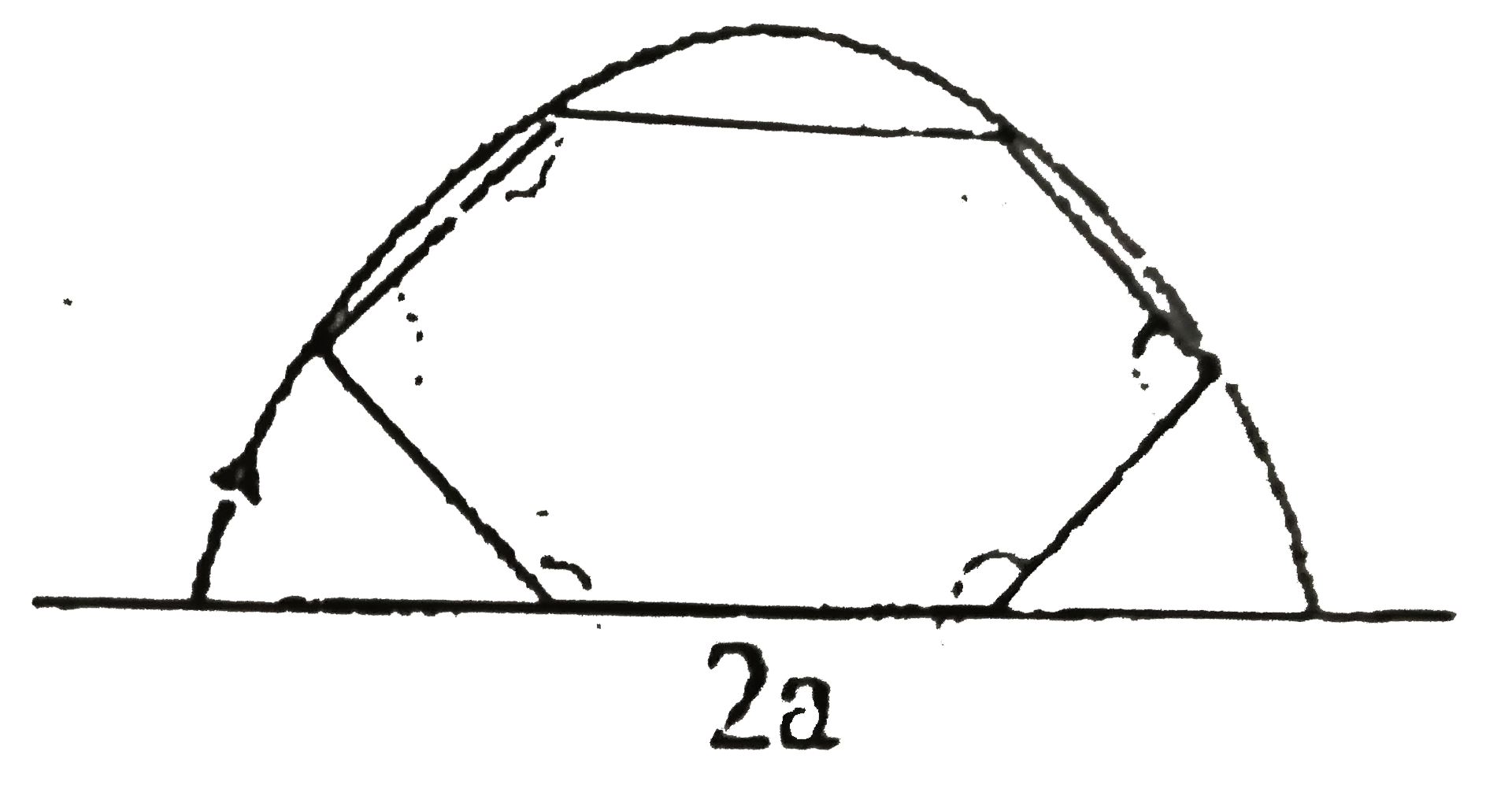
A particle is projected from the ground so as to graze the four upper vertices of a regular hexagor, whose side is 2a and which is placed vertically with one side on the ground. What is the range on the ground.
What is the range on the ground.

A

3 7 a

B

7 a

C

2 7 a

D

3 a

Text Solution
Verified by Experts

ocr_image
x 0 = R ( 4 a cos 60 ∘ + 2 a ) 2
x 0 = R 2 - 2 a
y = tan θ x ( 1 - x R )
a 3 = tan θ x [ 1 - ( R 2 - 2 a ) R ]
2 a 3 = tan θ [ ( R 2 - 2 x ) ] + 2 a cos 60 ∘ [ 1 - R 2 - 2 a + a R ]
1 2 = ( R - 4 a ) R - 2 a [ R - R 2 + 2 a ] [ R - R 2 a ] = ( R - 4 a ) ( P - 2 a )
[ R + 4 a ] ( R + 2 a )
1 2 = R 2 - 16 a 2 R 2 - 4 a 2
R 2 - 4 a 2 = 4 R 2 - 32 a 2
R = 2 a 7

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A particle is projected from the ground so as to graze the four upper vertices of a regular hexagor, whose side is 2a and which is placed vertically with one side on the ground.
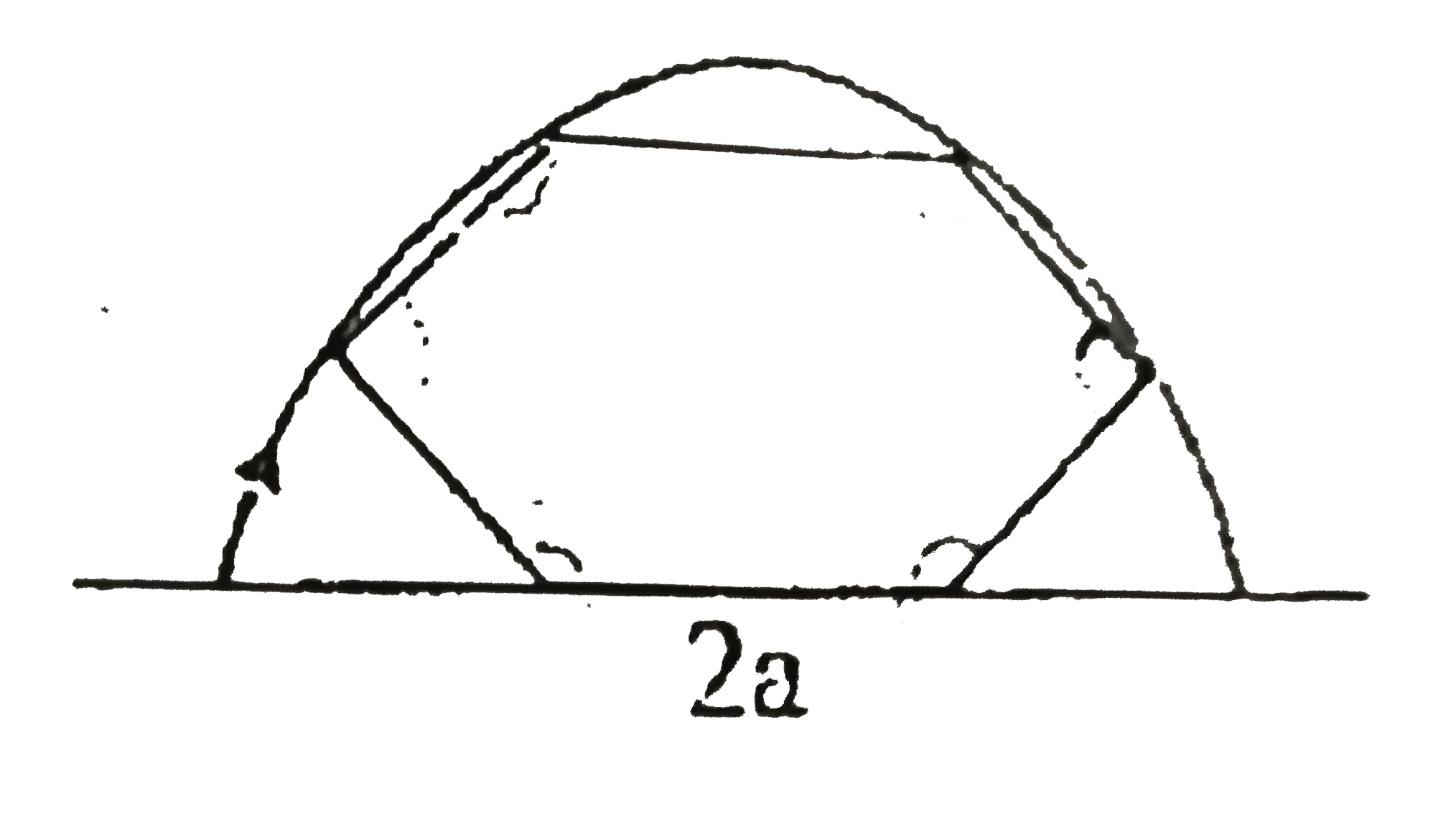
    ocr_image
    What is the ratio of the velocity of the particle on reaching the ground to the least velocity?

    A√313
    B√343
    C√163
    D√73

  • A ball is projected from the ground with velocity u such that its range is maximum Then

    AIts velocity at half the maximum height is √32u
    BIts velocity at the maximum height is u
    CChange in its velocity when it returns to the ground is u
    Dall the above are true

  • A particle is projected from ground with velocity 3ˆi+4ˆi m/s. Find range of the projectile :-

    A1.2m
    B3.6m
    C2.4m
    D10m