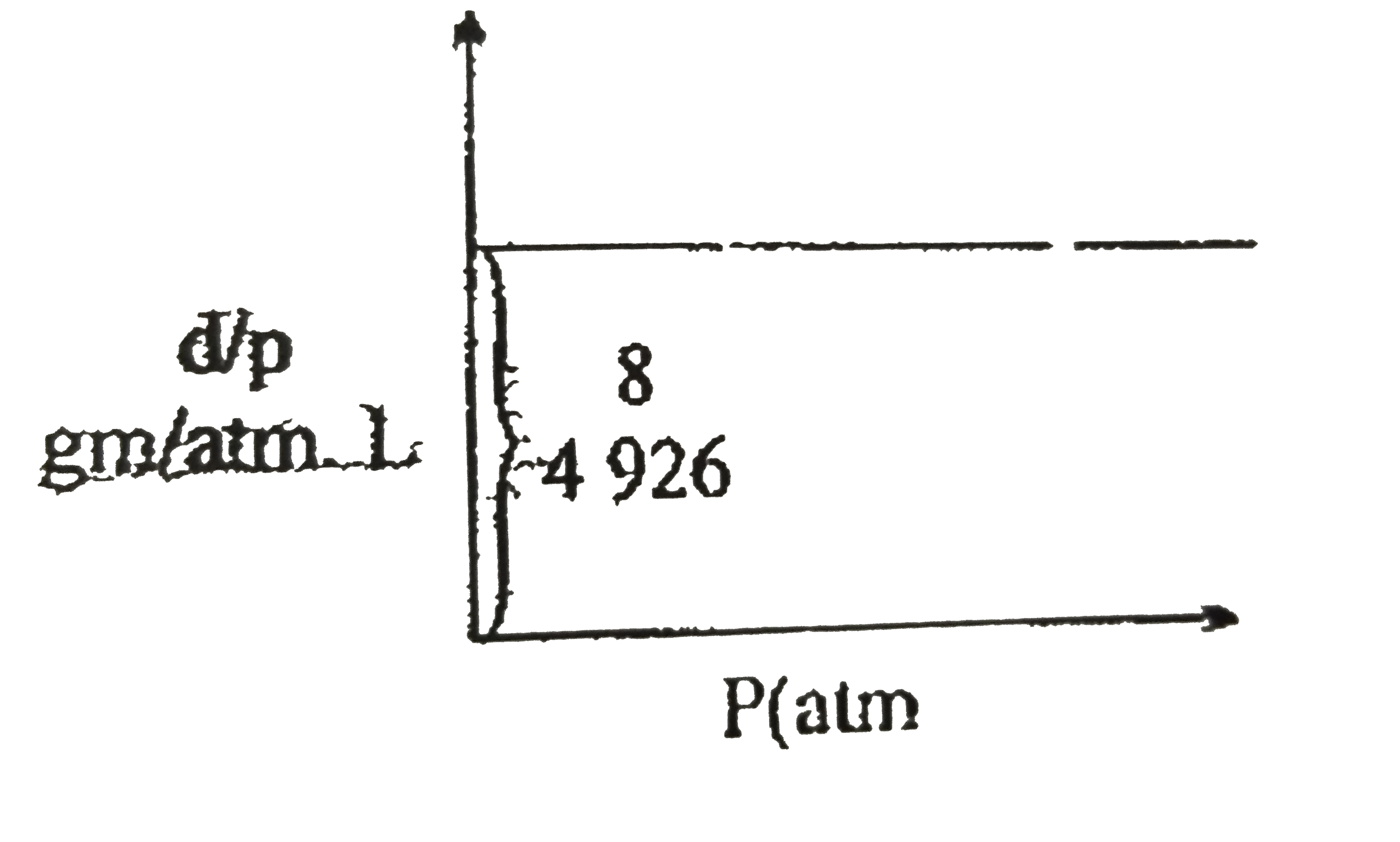
From the graph of dP vs P at a constant temperature of 300K. Calculate molar mass of the gas.
[Give R=0.0821 atm lit/mole-k]
![From the graph of (d)/(P) vs P at a constant temperature of 300K. Calculate molar mass of the gas. [Give R=0.0821 atm lit/mole-k]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_XI_RT_P2_E01_500_Q01.png)
Video Solution
Text Solution
PV=nRT
d=PMRT
dP=MRT
MRT=84.926
M=84.926×0.0821×300=40
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY PART (A)14videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY PART (B)1videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Chemistry PART D4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SOLUTIONSEXERCISE - Exercise432videos
SOLUTIONS
- BOOK - BANSALCHAPTER - THERMOCHEMISTRYEXERCISE - Exercise 415videos
THERMOCHEMISTRY
Similar Questions
Knowledge Check
- Question 1 - Select One or More
The graph of P vs V is given at temperature and number of moles :

The correct relationship is/areAT1>T2>T3BT1<T2<T3Cn1>n2>n3Dn3>n2>n1 - Question 2 - Select One
CH4 gas is behaving non-ideally. Compressibility factor for gas is 1.5 at 2 atm, 400K. Calculate molar volume for gas: [Given: R=0.08Litre−atmK−mole]
A24 litreB16 litreC48 litreD8 litre - Question 3 - Select One
A cylinder contains oxygen at pressure of 28 atm and at a temperature of 300 K. the mass of oxygen the gas, the pressure is found to be 7 atm and the temperature is 200 K. what mass of the gas has been used?
A100 gmB250 gmC625 gmD1000 gm
Osmotic pressue of a solution is 0.0821 atm at a temperature of 400 K. Calculate concerntration of solution in moles /litre.
View SolutionThe density of a gas is found to be 3.43 g/litre at 300K and 1.00 atm pressure. Calculate the molar mass of the gas.
View SolutionA container consists of 1 mole of liquid water and 1 mole of N2(g), at a temperature of 300K. If aqueous tension of water at 300K is 38mm of Hg and the contaienr is fitted with a piston operating at 0.1321 atm then calculate volume occupied by N2 gas:
(R=0.0821atm L/molk)View Solution80 gm of SOx gas occupies 15 litre at 2atm and 300K. The value of x is : (Given: R= 0.08 L-atm/K-mole)
View SolutionThe urms of a gas at 300K is 3R1/2 The molar mass of the gas in kgmo1−1 is .
View Solution


