यह मानिए कि एक कण जिसका द्रव्यमान m है वह स्थितिज ऊर्जा U=kx22+Ae−ax2 के साथ गति कर रहा है। जब यह x = a पर होता है, तो इसका वेग, va होता है जहाँ , A तथा α अचर है। कण मूल बिन्दु को पार करने में समर्थ होगा, यदि
A≥mv2a+ka22(1−e−αa2)
A≤mv2a+ka22(1−e−αa2)
A≤mv2a+ka2(1−e−αa2)
A≥mv2a+ka2(1−e−αa2)
The correct Answer is:B
ऊर्जा संरक्षण, किसी कण की कुल ऊर्जा सदैव नियत रहती है |
माना केंद्र x=0
∴TE(x=0)=TE(x=a)
अथार्त PEx+KXx=PE(x=a)+KE(x=a)
K(0)22+Ae−α×02KE(x=0)
=Ka22+Ae−α2+12mv2a
अथार्त A+KE(x=0)=Ka22+Ae−αa2+12mv2a
इसलिए A≤Ka22+Ae−αa2+12mv2a
[∴KE(x=0) अज्ञात है, A<RHS, यदि KE(x=0)=0,A=RHS]
अथार्त A(1−eαa2)≤ka2+mv2a2
अथार्त A<ka2+mv2a2(1−eαa2)
Topper's Solved these Questions
Similar Questions
किग्रा द्रव्यमान का एक ब्लॉक x- अक्ष पर गतिमान है इस पर कार्यरत बल F चित्रनुसार है। समय t = 2 सेकण्ड पर ब्लॉक का वेग -3मी /से है , तो समय t = 4 सेकण्ड पर ब्लॉक की चाल क्या होगी ?
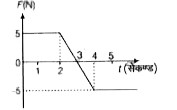 04:10View Solution
04:10View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
02:05View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
05:40View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionएक ठोस यौगिक X को गर्म करने पर यह CO2 गैस और एक अवशिष्ट देता है। अवशिष्ट जल के साथ मिश्रित होकर Y बनाता है। जल में Y के माध्यम से CO2 आधिक्य को गुजारने पर एक स्वच्छ विलयन Z प्राप्त होता है। Z को उबलने पर, यौगिक X का पुनः निर्माण होता है। यौगिक X है
View Solutionजब MnO_(2) को KOH के साथ संगलित किया जाता है, तब एक रंगीन यौगिक का निर्माण होता है। यौगिक और इसका रंग है:
View Solutionजब एसीटैल्डिहाइड को फेहलिंग विलयन के साथ उपचारित किया जाता है, तो यह निम्नलिखित में से किसका अवक्षेप देता है?
View Solutionजब P_2O_5 को जल के साथ गर्म किया जाता है, तो यह देता है
View Solutionयदि एक विशिष्ट विलायक में, एक यौगिक द्वारा समतल ध्रुवित प्रकाश का कोई घूर्णन नहीं होता है, यद्यपि यह किरैल है, तो इसका अर्थ हो सकता है कि
View Solutionहाइड्रोजन के समान एक काल्पनिक परमाणु के लिए, निकाय की स्थितिज ऊर्जा U (1) = (-ke^2)/(r^3) द्वारा दी जाती है, जहाँ r दो कणों के बीच की दूरी है। यदि कोणीय संवेग के क्वान्टीकरण का बोर मॉडल लागू होता है, तो कण का वेग निम्नलिखत में किसके द्वारा दिया जाता है?
View Solutionपरॉक्साइड आयन के लिए कौन सा कथन सही है?
(1) इसमें पाँच पूर्ण पूरित प्रति-बंधित आण्विक कक्षक होते हैं
(2) यह प्रतिचुंबकीय होता है
(3) इसकी बंध कोटि एक होती है
(4) यह नियॉन के साथ समइलेक्ट्रॉनी होता हैView Solutionक्लोरीन, दो समस्थानिक रूपों CI-37 और CI-35 में उपस्थित होता है, लेकिन इसका परमाणु द्रव्यमान 35.5 होता है। यह दर्शाता है कि CI-37 और CI-35 का अनुपात लगभग होता है:
View Solutionजब प्लास्टर ऑफ पेरिस, जल के संपर्क में आता है तो यह एक कठोर द्रव्यमान में बदल जाता है। कठोर द्रव्यमान का संघटन है:
View Solutionजब एक सल्फर सॉल वाष्पित होता है, तब सल्फर प्राप्त होता है। जल के साथ मिश्रित करने पर सल्फर सॉल निर्मित नहीं होता है। सॉल है:
View Solution

