A thin uniform rod of length L is resting against a wall and the floor as shown in the figure. Its lower end A is pulled towards left with a constant velocity v. Then the downward velocity v' of the other end B when the rod makes an angle θ with the floor is

v
v cos θ
v sin θ
v cotθ
The correct Answer is:D
According to the question,

Given, length of the uniform rod = L
the angle between rod and floor = θ
the angle between wall and floor = 90∘
Let the distance between point O to A is x and the distance between point O to B is y.
Now, By the velocity displacement relation w.r.t.t
v=dxdt ....(i)
and v. = - dydt ...(2)
(- negative sign denoted that y is decreasing. ) futher, x2+y2=L2 [ From the figure ]
Differentiating above equation w.t.t,,time t,
∴2xdxdt+2ydydx=0
Now, putting the values of dxdtanddydtfrom Eqs. (i) and (ii), we get
∴ xv = yv. or v. = xyv
or v. = v cot θ [from the figure ∴cotθ=xy]
So, the downward velocity of the other end B when the rod makes an angle θ with the floor is v.=vcotθ.
Similar Questions
Figure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View Solution
Knowledge Check
A thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
A√2glB√3glC√5glD√mgl
Figure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity u. As a result of this, end A starts moving down along the wall. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View Solution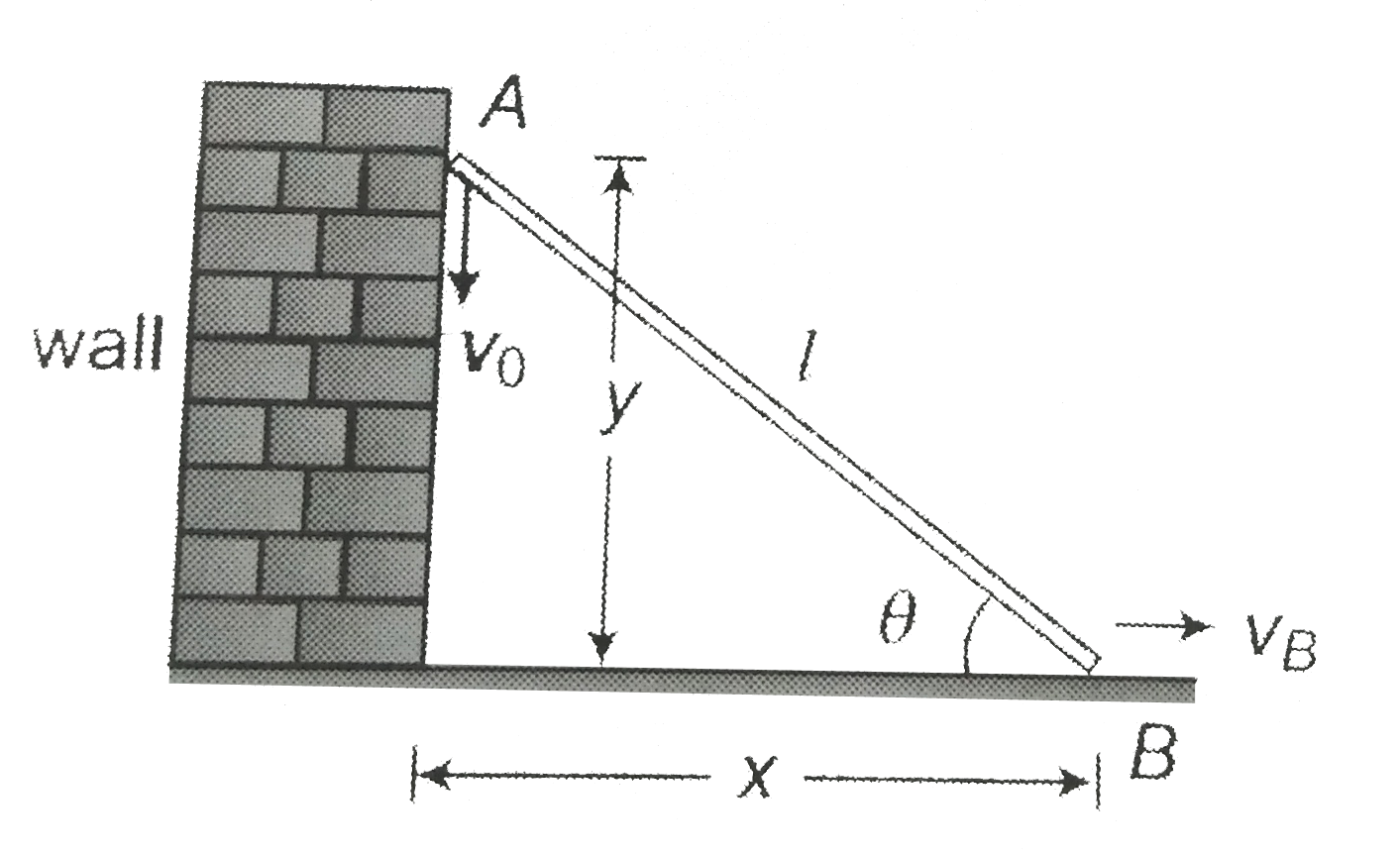
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v0 in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle θ with horizontal
View SolutionA rod of length 'l' is inclined at an angle 'theta' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1 what is the velocity of end B at the instant when rod makes 'theta' angle with the horizontal .
View Solution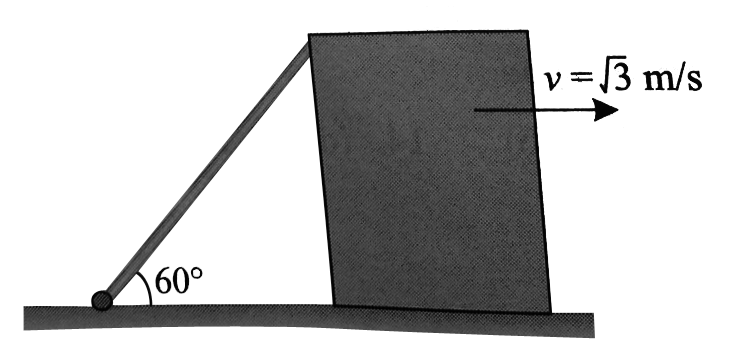
A rod AB is shown in figure. End A of the rod is fixed on ground. Block is moving with velocity √3 m/s towards right. The velocity of end B of rod when rod makes an angle of 60∘ with ground is :
View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View SolutionA thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
View Solution
