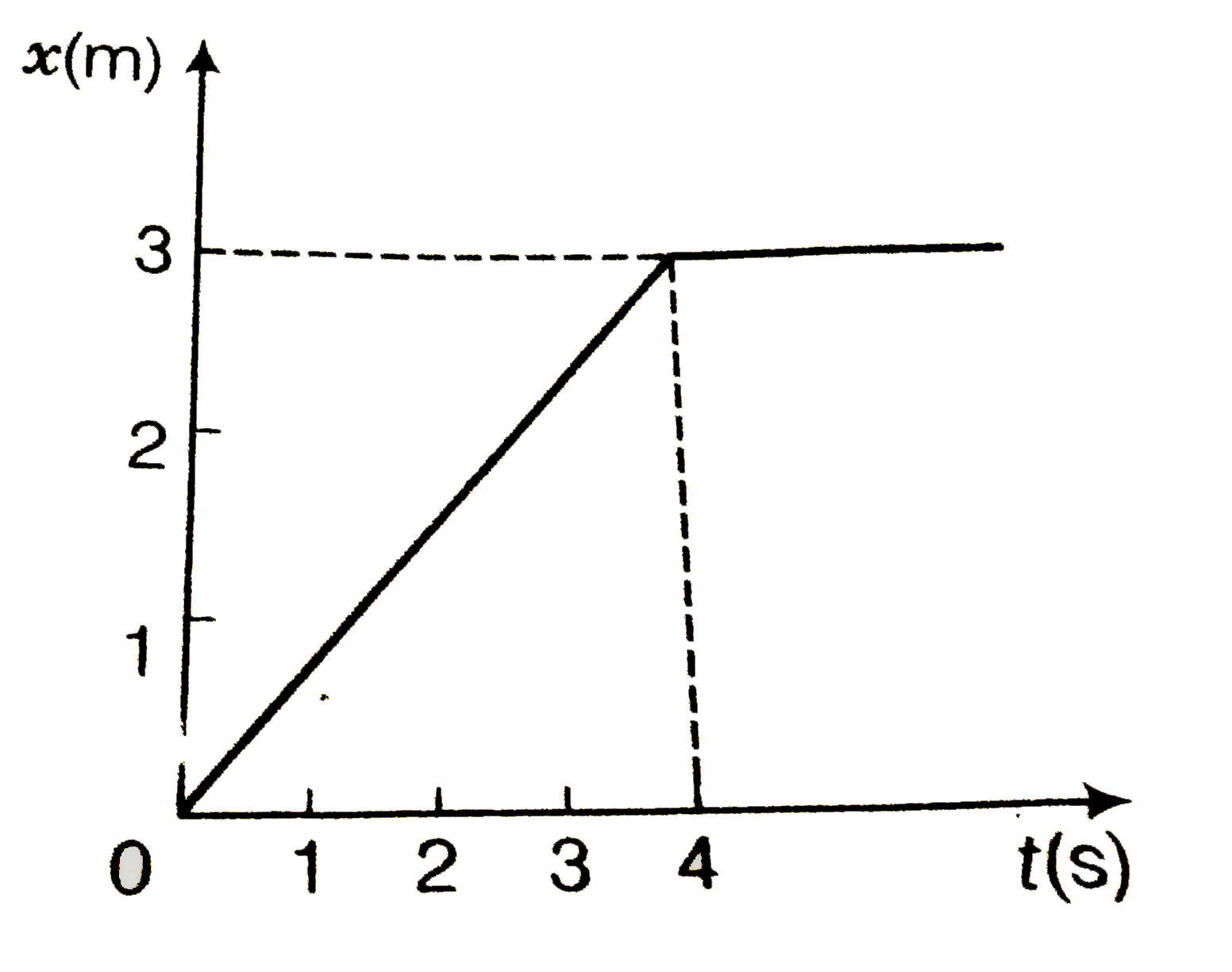
The position- time (x - t) graph of a moving baby of mass 2 kg is shown in the figure. The impulse on the body at t=4s is

A
1.5kg−ms−1
B
−1.5kg−ms−1
C
1kg−ms−1
D
2kg−ms−1
Text Solution
The correct Answer is:B
Here, mass of the body, m=2kg and time, t=4s
Impulse =pf−pi
where , pi= initial momentum,
pf= final momentum
Impulse =mvf−mvi=m(vf−vi)(∵p=mv)
As from the graph,
vf=3−38−4=0andvi=3−04−0=34
Impulse =2×(0−34)=−1.5 kg−ms−1
Hence, the correct option is (b).
|
Topper's Solved these Questions
- AP EAMCET SOLVED PAPER 2018 ( 23-04-2019,SHIFT -1)BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET SOLVED PAPER 2018 ( 23-04-2019,SHIFT -1)EXERCISE - Physics
40 Videos
- AP EAMCET SOLVED PAPER 2019 (22-04-2019, SHIFT-2)BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET SOLVED PAPER 2019 (22-04-2019, SHIFT-2)EXERCISE - PHYSICS
40 Videos
Similar Questions
Knowledge Check
The position-time graph of a particle of mass 0.1 kg is shown. The impulse at t = 2s is :
 A0.2kgms−1B0.02kgms−1C0.1kgms−1D0.4kgms−1
A0.2kgms−1B0.02kgms−1C0.1kgms−1D0.4kgms−1The position time graph of a body of mass 2kg is as given in What is the impulse on the body at t=0 s and t=4s ?
 . A23kgms−1B−23kgms−1C32kgms−1D−32kgms−1
. A23kgms−1B−23kgms−1C32kgms−1D−32kgms−1The position-time graph of a body of mass 0.04kg is shown in the figure. The time between two consecutive impulses received by the body and the magnitude of each impulse is
 A4sec,4×10−4kgm/sB2sec,8×10−4kgm/sC6sec,4×10−4kgm/sD8sec,8×10−4kgm/s
A4sec,4×10−4kgm/sB2sec,8×10−4kgm/sC6sec,4×10−4kgm/sD8sec,8×10−4kgm/s
The position time graph of a body of mass 2kg is as given in What is the impulse on the body at t=0 s and t=4s ?
 .
.
View SolutionPosition time graph of a particle of mass 2 kg is shown in figrure. Total work done on the particle from t=0 to t=4s is

View SolutionThe position (X)-time (t) graph for a particle of mass 1 kg moving along x-axis is shown in figure. Find impulse on particle at t = 4 s.
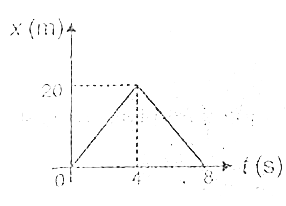
View SolutionThe position (X)-time (t) graph for a particle of mass 1 kg moving along x-axis is shown in figure. Find impulse on particle at t = 4 s.
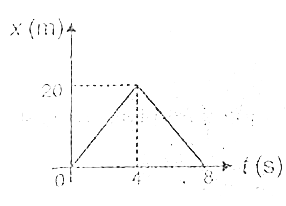
View SolutionPosition time graph of a particle of mass 2 kg is shown in figrure. Total work done on the particle from t=0 to t=4s is

View Solution