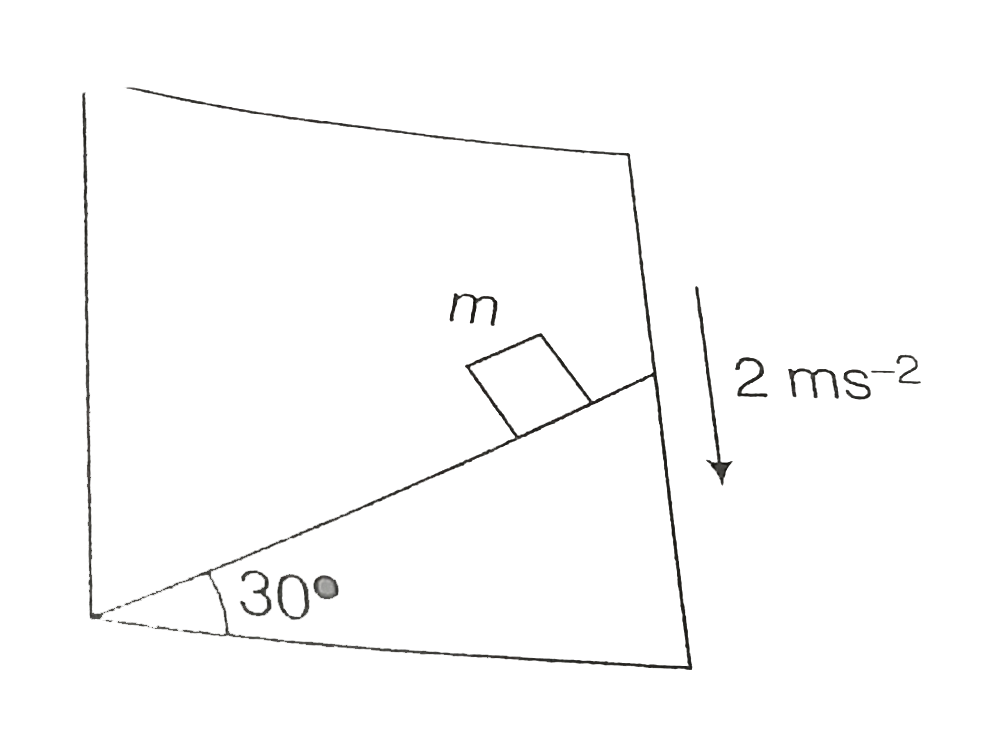
A block of mass m is lying on a rough inclined pla ne having an inclination The inclined plane is moving horzontally with a constant acceleration of as shown in the figure. The minimum value of coefficient of friction, so that the block remains stationary with respect to the inclined plane is (Take,

The correct Answer is:B
The block-plane system is shown in the figure,

So, from the above free body diagram (FBD), downward acceleration,
and the upward or opposing acceleration,
For block to be stationary,
[ from Eqs. (i) and (ii) ]
Divided the Eq. (iii) by sin and putting the values,
Hence, the correct option is (b)
Topper's Solved these Questions
- AP EAMCET SOLVED PAPER 2018 ( 23-04-2019,SHIFT -1)BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET SOLVED PAPER 2018 ( 23-04-2019,SHIFT -1)EXERCISE - Physics
40 Videos
- AP EAMCET SOLVED PAPER 2019 (22-04-2019, SHIFT-2)BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET SOLVED PAPER 2019 (22-04-2019, SHIFT-2)EXERCISE - PHYSICS
40 Videos
Similar Questions
A block of mass m is lying on a wedge having inclination angle α=tan−1(15) wedge is moving with a constant acceleration a=2ms−2 The minimum value of coefficient of friction μ so that m remain stationary w.r.t. wedge is

View SolutionA block of mass is kept on an inclined plane of a lift moving down with acceleration of 2ms−2 What should be the minimum coefficient of friction to let the block move down with constant velocity?

View Solution
Knowledge Check
A block of mass m is lying on a wedge having inclination angle α=tan−1(15) wedge is moving with a constant acceleration a=2ms−2 The minimum value of coefficient of friction μ so that m remain stationary w.r.t. wedge is
 A2/9B5/12C1/5D2/5
A2/9B5/12C1/5D2/5A block of mass is kept on an inclined plane of a lift moving down with acceleration of 2ms−2 What should be the minimum coefficient of friction to let the block move down with constant velocity?
 Aμ=1√3Bμ=0.4Cμ=0.8Dμ= not defined
Aμ=1√3Bμ=0.4Cμ=0.8Dμ= not definedA block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
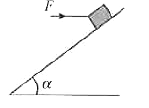 ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
A block of mass m is placed on an inclined plane which is moving with constant velocity v in horizontal direction as shown in figure. Then find out work done by the friction in time t if the block is at rest with respect to the incline plane.
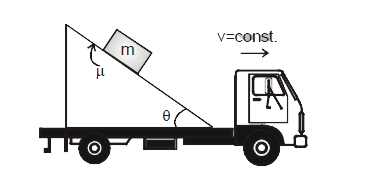
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

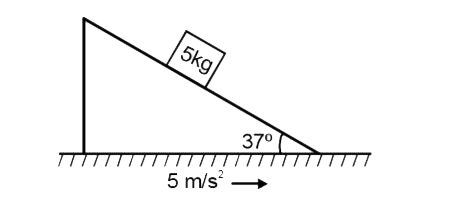
View SolutionInclined plane is moved towards right with an acceleration of 5ms−2 as shown in figure. Find force in newton which block of mass 5 kg exerts on the incline plane. ( All surface are smooth)
View SolutionA block of mass m is kept on an inclined plane of a lift moving down with acceleration of 2ms−1.What should be the coefficient of friction to let the block move down with constant velocity relative to lift.
View Solution
