A spherical body of density $ρ$ is floating half immersed in liquid of density d, if $α$ is the surface tension of the liquid, then the diameter of the body is

A

$\sqrt{\frac{3 α}{g (2 ρ - d)}}$

B

$\sqrt{\frac{6 σ}{g (2 ρ - d)}}$

C

$\sqrt{\frac{4 σ}{g (2 p - d)}}$

D

$\sqrt{\frac{12 σ}{g (2 ρ - d)}}$

Text Solution

Verified by Experts

The correct Answer is:A

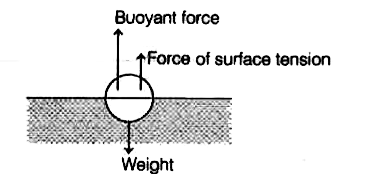
weight of body
= Bouyant force + Force of suface tension
$\frac{4}{3} π r^{3} ρ \times g = \frac{2}{3} π r^{3} d g + 2 π r δ$
$\frac{2}{3} π r^{3} g (2 ρ - d) = 2 π α$
$S o, r^{2} = \frac{3 α}{g (ρ 2 p - d)}$
So, $r = \frac{\sqrt{3 α}}{g (2 ρ - d)}$

|

Updated on:21/07/2023

Class 12 PHYSICS ONLINE QUESTION PAPER 2018

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A drop of liquid of density $ρ$ is floating half-immersed in a liquid of density $d$ . If $ρ$ is the surface tension the diameter of the drop of the liquid is
A $\frac{T A^{2}}{V}$
B $\frac{2 T A^{2}}{V}$
C $\frac{4 T A^{2}}{V}$
D $\frac{T A^{2}}{2 V}$
Question 2 - Select One
A drop of liquid of density $ρ$ is floating half-immersed in a liquid of density $d$ . If $ρ$ is the surface tension the diameter of the drop of the liquid is
A $\sqrt{\frac{σ}{g (2 ρ - d)}}$
B $\sqrt{\frac{2 σ}{g (2 ρ - d)}}$
C $\sqrt{\frac{6 σ}{g (2 ρ - d)}}$
D $\sqrt{\frac{12 σ}{g (2 ρ - d)}}$
Question 3 - Select One
A drop of liquid of density p is floating half-immersed in a liquid of density d. If σ is the surface tension, then the diameter of the drop of the liquid is
A $\sqrt{\frac{σ}{g (2 ρ - d)}}$
B $\sqrt{\frac{2 σ}{g (2 ρ - d)}}$
C $\sqrt{\frac{8 σ}{g (2 ρ - d)}}$
D $\sqrt{\frac{12 σ}{g (2 ρ - d)}}$

TS EAMCET PREVIOUS YEAR PAPERS-ONLINE QUESTION PAPER 2018-PHYSICS

Home
Ask Doubt
Profile