A body of density sinks in a liquid of density .The densities and are related as:
The correct Answer is:C
To solve the problem, we need to establish the relationship between the density of the body (ρ) and the density of the liquid (ρ_L) based on the information provided.
1. Understanding the Problem:
- We have a body with a density denoted as ρ.
- The liquid in which the body is submerged has a density denoted as ρ_L.
- The problem states that the body sinks in the liquid.
2. Applying Archimedes' Principle:
- According to Archimedes' Principle, a body will float in a fluid if its density is less than the density of the fluid. Conversely, if the body sinks, its density must be greater than the density of the fluid.
3. Establishing the Relationship:
- Since the body is sinking, we can conclude that the density of the body (ρ) is greater than the density of the liquid (ρ_L).
- Mathematically, this can be expressed as:
ρ>ρL
4. Conclusion:
- Therefore, the relationship between the densities is that the density of the body is greater than the density of the liquid.
Final Answer:
The relationship between the densities is:
ρ>ρL
- We have a body with a density denoted as ρ.
- The liquid in which the body is submerged has a density denoted as ρ_L.
- The problem states that the body sinks in the liquid.
- According to Archimedes' Principle, a body will float in a fluid if its density is less than the density of the fluid. Conversely, if the body sinks, its density must be greater than the density of the fluid.
- Since the body is sinking, we can conclude that the density of the body (ρ) is greater than the density of the liquid (ρ_L).
- Mathematically, this can be expressed as:
ρ>ρL
- Therefore, the relationship between the densities is that the density of the body is greater than the density of the liquid.
The relationship between the densities is:
ρ>ρL
Topper's Solved these Questions
- BOOK - ICSECHAPTER - UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONEXERCISE - EXERCISE 5(A) (Numerical)10videos
UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATION
- BOOK - ICSECHAPTER - UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONEXERCISE - EXERCISE 5(B)18videos
UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATION
- BOOK - ICSECHAPTER - UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONEXERCISE - EXERCISE 5(A)28videos
UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATION
- BOOK - ICSECHAPTER - SOUNDEXERCISE - TOPIC 2 Infrasonic and Ultrasonic Waves ( 3 Marks Questions)3videos
SOUND
Similar Questions
Knowledge Check
- Question 1 - Select One
A body floats in a liquid A of density ρ1 with a part of it submerged inside liquid while in liquid B of density ρ2 totally submerged inside liquid. The densities ρ1 and ρ2 are related as :
Aρ1=ρ2Bρ1<ρ2Cρ1>ρ2Dnothing can be said - Question 2 - Select One
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
A body of volume V and density ρ is kept completely immersed in a liquid of density ρL. If g is the acceleration due to gravity, write expressions for the following
(i) the weight of the body.
(ii) the upthrust on the body.
(iii) the apparent weight of the body in liquid,
(iv) the loss in weight of the body.View SolutionAssertion : A solid is floating in a liquid of density ρ1. When the solid melts its density becomes ρ2 in liquid state. If ρ1>ρ2 level of liquids will increase after melting.
Reason : In liquid state volume always increases after a solid melts.View SolutionTwo wooden blocks A and B float in a liquid of density ρL as shown. The distance L and H are shown. After some time, block B falls into the liquid, so that L decreases and H increases. If density of block B is ρB, find the correct option.
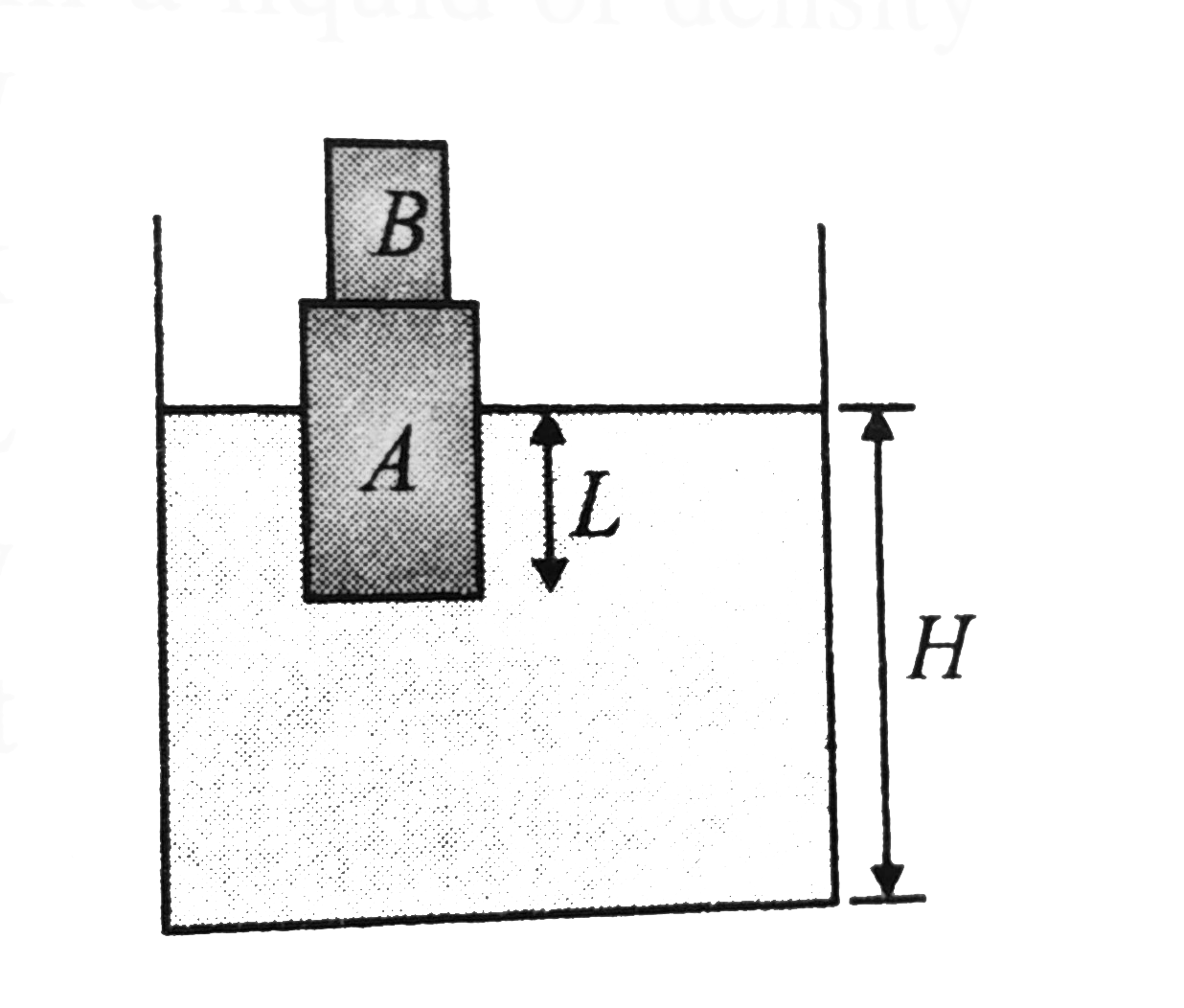 View Solution
View SolutionA cubical block of density ρ floats completely immersed in two non-mixing liquids of densities ρ1andρ2 as shown in figure. The relation between ρ,ρ1andρ2 is :
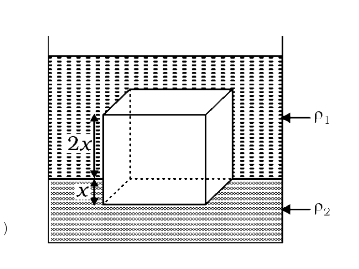 View Solution
View SolutionA ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
View SolutionA rectangular tube of uniform cross section has three liquids of densities ρ1,ρ2 and ρ3. Each liquid column has length l equal to length of sides of the equilateral triangle. Find the length x of the liquid of density ρ1 in the horizontal limb of the tube, if the triangular tube is kept in the vertical plane.
 View Solution
View Solution

